​ 2019，被大多数温暖环绕，偶尔一些人生瞬间变得冰冷和坚硬，无法躲避。但还好，一切终将过去。总的来说，2019并不简单，生活频繁出拳（胖虎的300斤铁拳，直立对打，凭着经验和运气躲过一些，另外一些结结实实地砸在脸上。可以说每一拳都不含糊，一击重拳，甚至可以感受到在脸上凝固停滞的拳气。不过今年也算是和生活对过几招了，本想着步步清风认真生活，凭阅历自撰一本《人间攻略》，大摇大摆地走上建设社会的征途，没想到生活反手甩一本《人间骚浪贱指南》，害，2019全线崩溃，2020推倒重来，希望今年和生活再次交手能从容一些了。

「说真的，你将来打算怎么办呢？」「我打算喝完这一杯」

研究生毕业失与得

1. 毕业

研究生三年，形象地说， 从一个小池塘跳到另外一个小池塘中，激起一朵Information Sciences期刊论文小浪花，然后扑通入水无踪影，从二十几岁精壮小伙想掏空世界的功利心来看，不值当。很难想象，这朵靠着身体抽搐翻腾出来小破花有多艰难，为啥别人的象牙塔是导师领进豪华直升电梯，直通塔顶，而我们要一步一爬，唉哟连特么象牙塔都是自己垒起来的，还好最后实验室人手一篇领域(次)顶刊，纷纷告别科研学术，有着不错的工作落脚处，也算是纯粹地感受了一把学术上知其然也知其所以然过程，人生历程多了一份体验，虽然不符预期，但也感激经历。

学校这几年忙忙忙，感觉也没忙出啥东西来，没发展别的兴趣，甜甜的恋爱还是没轮到我，好像蓝色大门里说的「 夏天就要过去了，我们好像什么都没做」「 是啊，就这样跑来跑去，什么都没做 」「那总会留下些什么吧，留下了什么，我们就会成为怎么样的大人 」

真要说有哪些值得关注的改变话，觉得还是有一些：

• 喜欢上了摇滚乐
• 性格从怂包变得小型社恐（到今天似乎消除了，大家都一样，五五开）
• 资源搜索能力加强，有需要的东西可以独立自学
• 处理感情还是一塌糊涂，不能成熟表达爱与索取爱
• 总在试探，都在权衡，消散热爱的能力

毕业的话，希望自己的期刊论文每年多一次引用吧，谷歌学术搜索排名能前一点，这个新年学术愿望不过分吧。

1. 就业

面试造火箭，上班拧螺丝的故事早有耳闻，人力小姐姐萝莉外表杀人诛心可不含糊，论实力与面试的迷一样的相关函数，求职路上太多有意思的故事了，这一路也不容易。

忙着论文错过了秋招，磕磕碰碰地走上春招这条血路，太难了呀，简直比沥青未干的蜀道还难！一场场大型面试崩溃招聘现场， 黑压压一片学生，排着队递简历，精神上首先就完了。投了简历石沉大海，回来路上，真的是天空突然一道光打在你身上，自我怀疑的高光时刻。二十五岁这场人生三分之一考试，每次到交答卷才发现真的准备的不够充分。春招凭着发表的论文和一些算法竞赛的获奖，获得较多的面试机会，磕磕碰碰，沉舟侧畔，最后也算成功上岸了，有两个比较有印象的故事：

1）投了一些大厂算法类的岗位无果后，参加了一个猎头帮改简历的招聘会，那天去的早， 现场没啥人，改完简历后和猎头大叔聊了起来，咔咔咔一顿哭诉当代年轻人的不容易，委屈大王，心酸2019，为啥生活不如意都落我这个失意年轻人的大头上！（那段时间感情状态、生活状态各方面真的是DOWN到深海几万里）。猎头大叔当时说啥我忘记了，总之谈了很久，他让我加油坚持，不要放低要求去小企业得以慰藉，年轻人要有年轻人的样子！我心中一顿爆暖，离开的时候还喊了我回来，握了握手，说很开心和我谈话。

2）一家基金公司，总裁面，到了给offer阶段，我说还有另外一家在考虑，她说来不来她这里没关系，年轻人找工作要好好考虑，要选对行业和团队，不要盯着一个岗位就上，并给了很多中肯的年轻人意见。我是很信仰人生经验攻略的，这些年一路过来，可太缺参考物了，最后没去还是很谢谢这些不给年轻人画饼，并愿意指导年轻人意见的大佬。

给毕业求职的同学一些建议：

1. 不要错过秋春招
2. 清楚自己的满意和愿意接受的岗位
3. 校招不像做饭，不需要等万事俱备才开始
4. 每次多总结复盘，打铁还需自身硬
5. 小心人力大姐

以上其实都是废话，多面几次自己就有谱了

不管怎样，还是顺利毕业了嘿！

自我管理

​ 1.睡眠

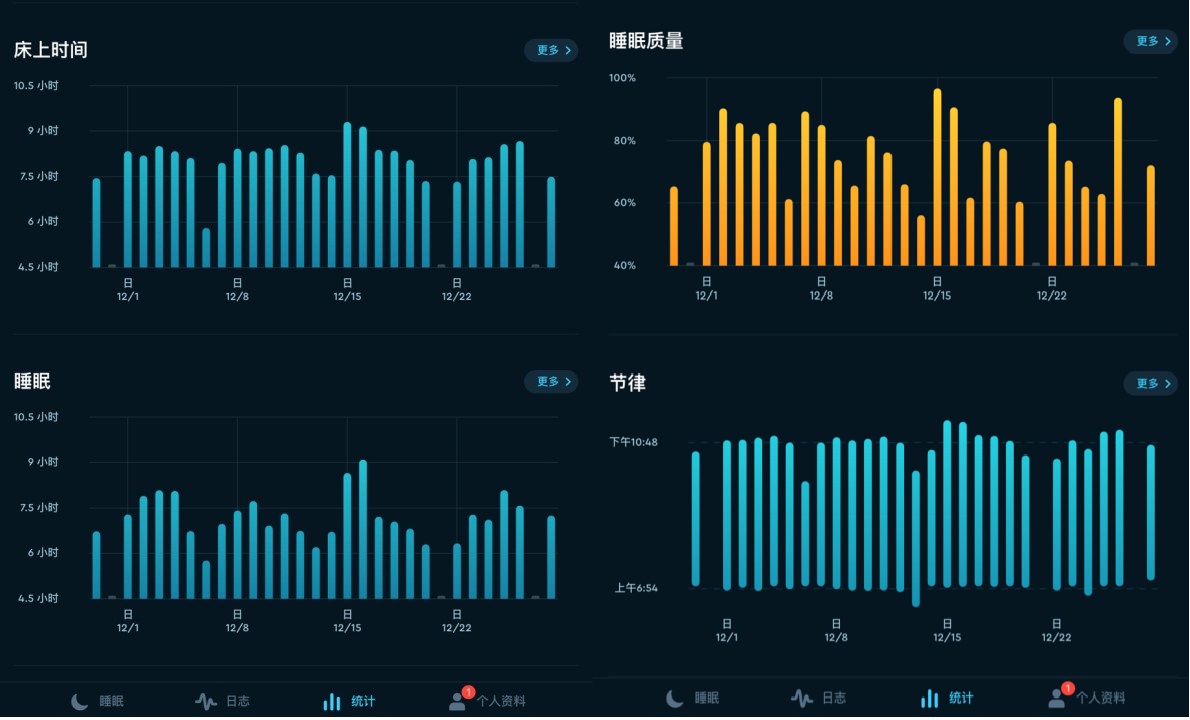
出来搬砖以来，睡眠变得规律很多，七点起床，十点半准时雇人敲晕自己。睡眠时间大概维持在七个半小时，午休半小时，持续搬砖问题不大。周末一般会把一周攒起来的抖音刷一遍，看看天地之间的沙雕，安心睡去。

1. 记账

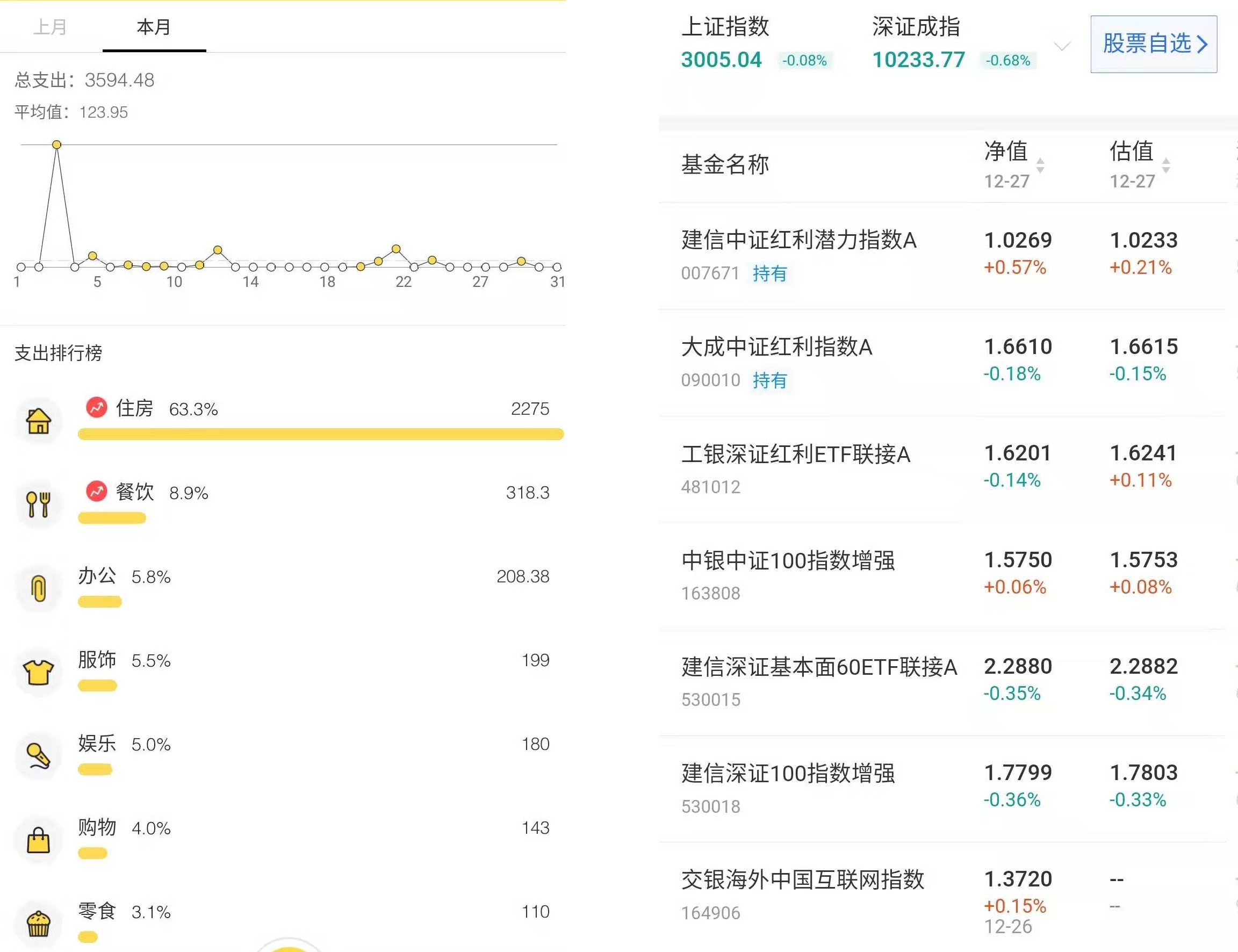
​ 不得不说，当代年轻人独立买房还是很艰难，看着每项支出其实也还好，但是汇到一起每月支出都会比想象的多，要是活动多一些也存不了几个钱。今年出来搬砖后，把银行和朋友借的钱都还清，自己日常支出也能稳定下来，这个感觉还是很棒的！

​ 定投指数基金，3000点入场，做一颗茁壮成长的韭菜！

1. 健康

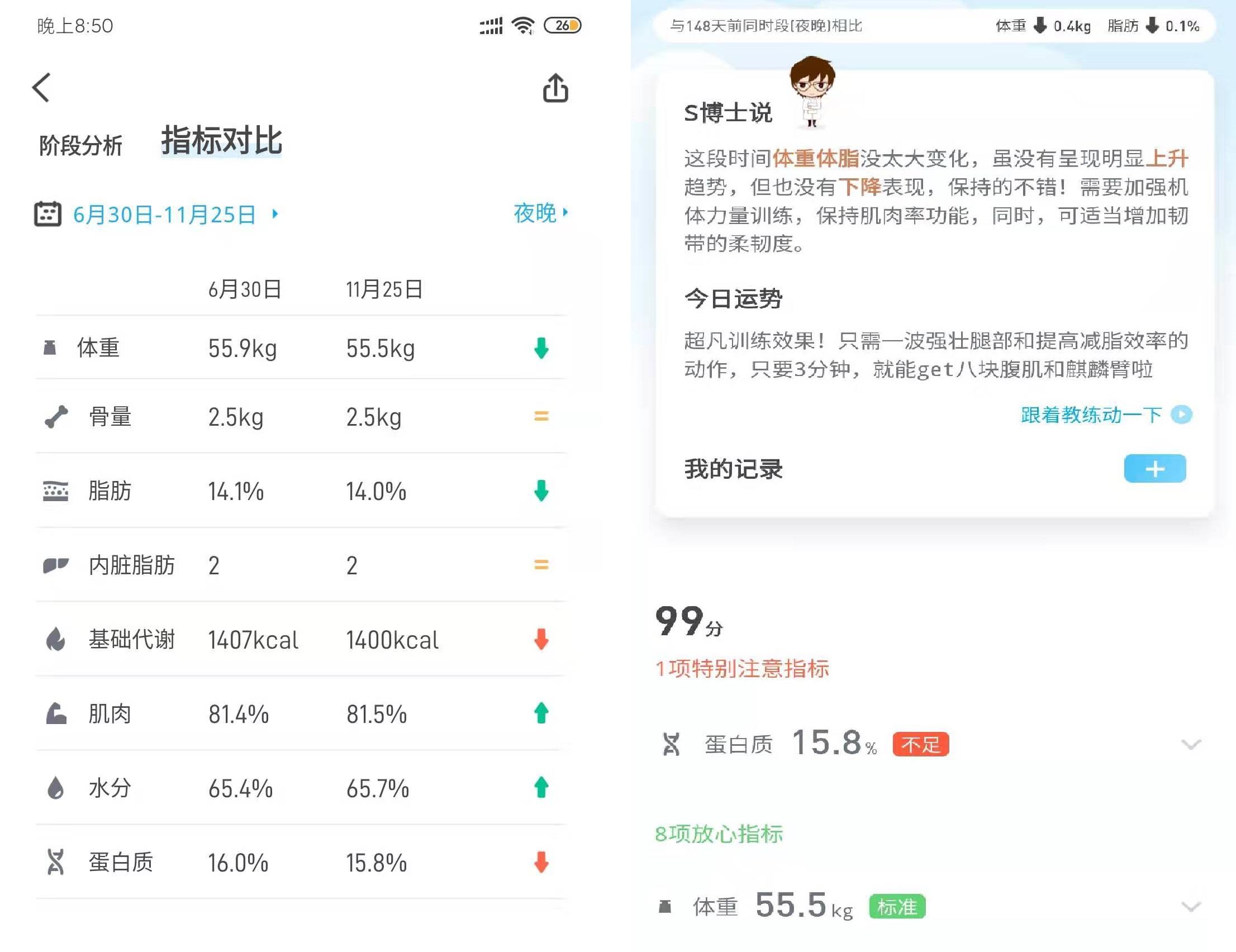
​ 今年做了个手术，还确诊了过敏性鼻炎，是要提醒自己该更加注意身体健康这一方面了。另外鼻炎应该是学校宿舍那台旧空调造成的，风口对着床吹，还滴水，每次在宿舍鼻子难受的不行，去到实验室马上就好了，弄到这个不治的毛病还是很痛苦的。目前的策略是上班走路走路走路！枸杞枸杞枸杞！泡脚泡脚泡脚！ 健身是没戏了，在学校都没能坚持下来，希望明年能坚持去游个泳吧。

关于书影音

​

五星电影：

• 极限职业（韩）
• 调音师（印度）
• 海蒂和爷爷（德）
• 复仇者联盟4（美）
• 摇摆狂潮（韩）

书籍：

• 《代码整洁之道—程序员的职业素养》
• 《代码整洁之道—Clean》
• 《黑客与画家》
• 《交换梦想》
• 《宇宙超度指南》
• 《如何成为一个厉害的人》

音乐演出

• 陈知游园惊梦 2019避雨屋檐巡演
• Brett乐队 2019巡演
• 文雀乐队 2019她从来不唱我们的歌巡演

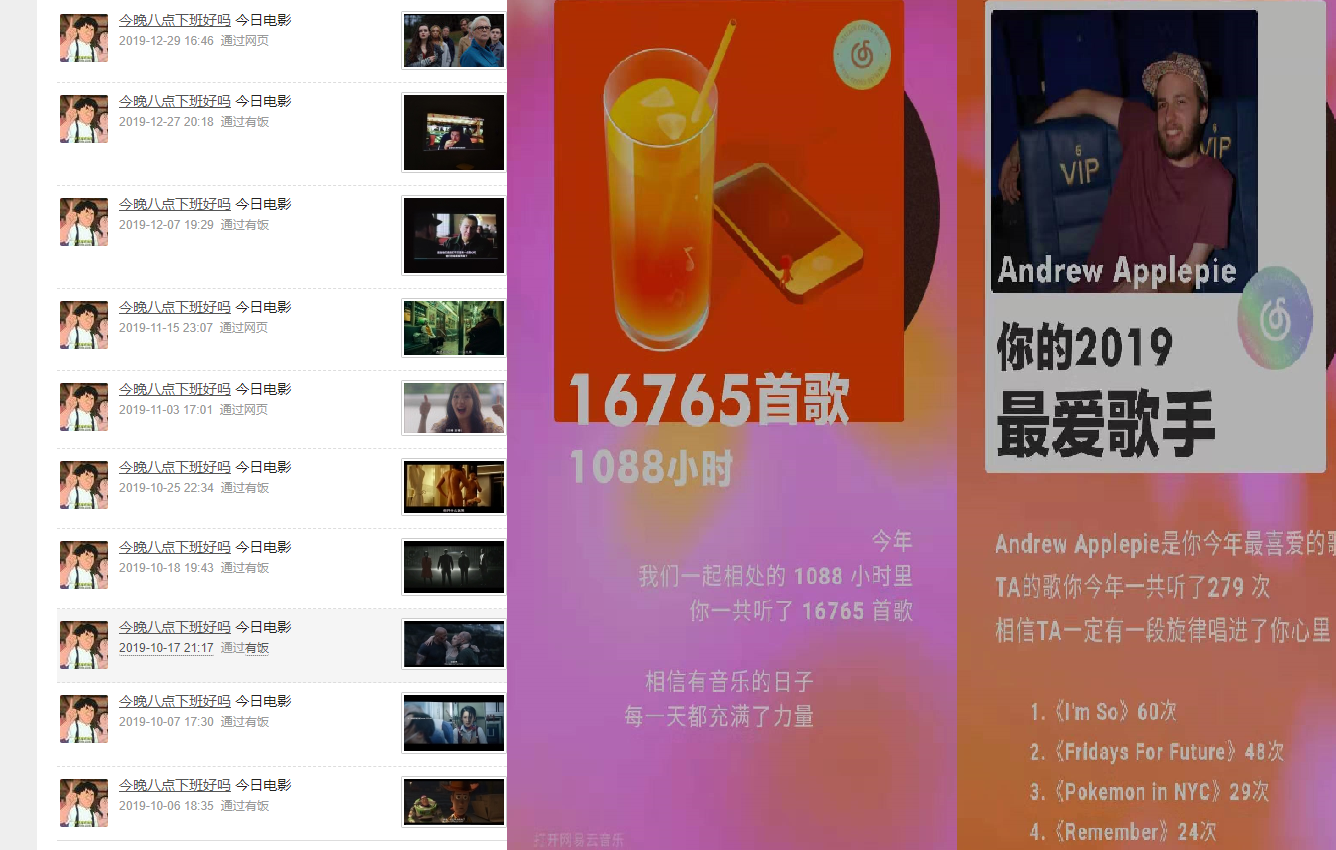
今年观影70+，还为观影事业买了个投影仪，每个周末的夜晚，100寸电子辐射的快乐，碳水化合物乐园，灵魂像膨化食品被打开时一样开心的裂开。听歌方面依然是摇滚为主，流行和民谣听一些，没想到居然Andrew Applepie成为了年度歌手，一度认为人类必须牵着手才能听Applepie，哎呀哎呀摇滚死了呀。

今年看书希望多看些编程类的工具书，数据库、理解框架是目前搬砖进阶的目标。

不要为今年读书太少而难过，去年你也没读多少

Flag！Flag！Flag！

• 希望今年可以更自信地表达自己

• 搬出来一个人住，养条狗，或养个女朋友

• 尝试视频内容创作

• 开源一个自己感兴趣的工程项目

• 逛一逛动物园，打卡深圳所有公园

• 存钱买老婆

总的来说，2019并不值得被总结，是经历当中最难的一年，有很多至暗时刻不愿提及，没必要铭记些什么，2019过去了就过去了。用一些不太恰当又很冗长的比喻就是， 就像聊了18个月的心理医生突然告诉你，我不能再给你做咨询了，因为我已经爱上你了； 就像一个易碎的老年人正盯着你并且缓缓插队，而你只好故作无睹 ；就像班上倒数第二辅导倒数第一课后习题，并且给出详细的解题思路 。2020不敢说万事顺利，希望新一年遇到的问题都是不太复杂自己慢慢能处理好的，新年加油！

新的一年，就不祝一帆风顺了，祝大家乘风破浪吧！

以上

在本章中，我们将看到循环神经网络背后的基本概念，他们所面临的主要问题（换句话说，在之前中讨论的消失／爆炸的梯度），以及广泛用于反抗这些问题的方法：LSTM 和 GRU cell（单元）。 循环神经网路主要解决带有时序性质的问题。

基本循环神经

看下图中一个简单的循环神经网络图，它由输入层、一个隐藏层和一个输出层组成。我们可以看到，循环神经网络的隐藏层的值s不仅仅取决于当前这次的输入x，还取决于上一次隐藏层的值s（结果向前和向后传播后的上一次这个位置的值）。

如果我们把上面的图展开，循环神经网络也可以画成下面这个样子：

现在看起来就清楚不少了，这个网络在t时刻接收到输入$X_t$之后，隐藏层的值是$S_t$，输出值是$o_t$。关键一点是，$s_t$的值不仅仅取决于$X_t$，还取决于$S_{t−1}$。我们可以使用下面的公式来表示循环神经网络的计算方法： (U,V,W都为权重)

式1是输出层的计算公式，输出层是一个全连接层，也就是它的每个节点都和隐藏层的每个节点相连。V是输出层的权重矩阵，g是激活函数。式2是隐藏层的计算公式，它是循环层。U是输入x的权重矩阵，W是上一次的值st−1st−1作为这一次的输入的权重矩阵，f是激活函数。

从上面的公式可以看出，循环层和全连接层的区别就是多了一个权重矩阵W。

若反复把式2代入带式1，我们将得到：

从上面可以看出，循环神经网络的输出值$o_t$，是受前面历次输入值$x_t$、$x_{t−1}$、$x_{t−2}$…的影响的，这就是为什么循环神经网络可以往前看任意多个输入值的原因。

再来看一个清晰一点的循环神经元层，见下图， 在每个时间步t，每个神经元都接收输入向量$x^{(t)}$和前一个时间步的输出向量$y^{(t−1)}$，如图所示。 请注意，输入和输出都是向量（当只有一个神经元时，输出是一个标量）。

每个循环神经元有两组权重：一组用于输入 $x^{(t)}$，另一组用于前一时间步长 $y^{(t−1)}$的输出。我们称这些权重向量为$w_x$和$w_y$。如下面公式所示（b是偏差项，φ(·)是激活函数，例如 ReLU），可以计算单个循环神经元的输出。

就像前馈神经网络一样，我们可以使用上一个公式的向量化形式，对整个小批量计算整个层的输出。

• $Y^{(t)}$是$m×n_{neurons}$矩阵，包含在最小批次中每个实例在时间步t处的层输出（m是小批次中的实例数， $n_{neurons}$是神经元数
• $X^{(t)}$是$m×n_{inputs}$矩阵，包含所有实例的输入的（$n_{inputs}$是输入特征的数量 ）
• $W_x$是$ n_{inputs}×n_{neurons} $矩阵，包含当前时间步的输入的连接权重的。
• $W_y$是$n_{neurons}×n_{neurons}$矩阵，包含上一个时间步的输出的连接权重。
• 权重矩阵$W_x$和$W_y$通常连接成单个矩阵W，形状为$(n_{inputs}+n_{neurons})×n_{neurons}$（见上述公式第二行）
• b是大小为 $n_{neurons}$的向量，包含每个神经元的偏置项

注意， 在第一个时间步，t = 0，没有以前的输出，所以它们通常被假定为全零。

TensorFlow 中的解释基本 RNN

首先，我们来实现一个非常简单的 RNN 模型，而不使用任何 TensorFlow 的 RNN 操作，以更好地理解发生了什么。 我们将使用 tanh 激活函数创建由 5 个循环神经元的循环层组成的 RNN（如下图所示的 RNN）。

我们将假设 RNN 只运行两个时间步，每个时间步输入大小为 3 的向量。 下面的代码构建了这个 RNN，展开了两个时间步骤：

1
2
3
4
5
6
7
8
9
10
11

n_inputs = 3
n_neurons = 5
X0 = tf.placeholder(tf.float32, [None, n_inputs])
# 充当经过向前向后传播后的下一时刻的输入值
X1 = tf.placeholder(tf.float32, [None, n_inputs]) 
Wx = tf.Variable(tf.random_normal(shape=[n_inputs, n_neurons], dtype=tf.float32))
Wy = tf.Variable(tf.random_normal(shape=[n_neurons, n_neurons], dtype=tf.float32))
b = tf.Variable(tf.zeros([1, n_neurons], dtype=tf.float32))
Y0 = tf.tanh(tf.matmul(X0, Wx) + b)
Y1 = tf.tanh(tf.matmul(Y0, Wy) + tf.matmul(X1, Wx) + b) # 主要理解这句
init = tf.global_variables_initializer()

双向循环神经网络

对于语言模型来说，很多时候光看前面的词是不够的，比如下面这句话：

我的手机坏了，我打算____一部新手机。

可以想象，如果我们只看横线前面的词，手机坏了，那么我是打算修一修？换一部新的？还是大哭一场？这些都是无法确定的，但是如果我们也看到了后面的词是“一部新手机”，那么横线上的词填“买”的概率就大很多了。

而这个在单向循环神经网络是无法建模的，因此我们需要双向循环神经网络，如下图所示：

我们先考虑$y_2$的计算，从上图可以看出，双向卷积神经网络的隐藏层要保存两个值，一个A参与正向计算，另一个A′参与反向计算。最终的输出值$y_2$取决于$A_2$和$A_2’$，其计算方法为：

$A_2$和$A_2’$ 则分别计算

现在，我们已经可以看出一般的规律：正向计算时，隐藏层的值$s_t$与$s_{t−1}$有关；反向计算时，隐藏层的值$s_t′$与$s′_{t+1}$有关；最终的输出取决于正向和反向计算的加和。现在，我们仿照式1和式2，写出双向循环神经网络的计算方法：

从上面三个公式我们可以看到，正向计算和反向计算不共享权重，也就是说U和U′、W和W′、V和V′都是不同的权重矩阵。

深度循环神经网络

前面我们介绍的循环神经网络只有一个隐藏层，我们当然也可以堆叠两个以上的隐藏层，这样就得到了深度循环神经网络。如下图所示

训练 RNN

为了训练一个 RNN，诀窍是在时间上展开（就像我们刚刚做的那样），然后简单地使用常规反向传播（见图 14-5）。 这个策略被称为时间上的标准反向传播（BPTT）。另外可以采用截断式沿时间反向传播算法（BPTT）可以降低循环网络中每项参数更新的复杂度。简而言之，此种算法可以让我们以同样的运算能力更快地定型神经网络 。假设用长度为12个时间步的时间序列定型一个循环网络。我们需要进行12步的正向传递，计算误差（基于预测与实际值对比），再进行12个时间步的反向传递：

就像在正常的反向传播中一样，展开的网络（用虚线箭头表示）有第一个正向传递。然后使用损失函数评估输出序列$C(Y_{t_{min}},Y_{t_{min+1}},…,Y_{t_{max}})$。其中$t_{min}$ 和$t_{max}$ 是第一个和最后一个输出时间步长，不计算忽略的输出），并且该损失函数的梯度通过展开的网络向后传播（实线箭头）；最后使用在 BPTT 期间计算的梯度来更新模型参数。 请注意，梯度在损失函数所使用的所有输出中反向流动，而不仅仅通过最终输出（截断式传播，例如，在图 14-5 中，损失函数使用网络的最后三个输出Y(2)，Y(3)，和Y(4)，所以梯度流经这三个输出，但不通过Y(0)和Y(1)。而且，由于在每个时间步骤使用相同的参数W和b，所以反向传播将做正确的事情并且总结所有时间步骤。

具体BPTT的解析过程可以看这篇戳我

训练序列分类器

我们训练一个 RNN 来分类 MNIST 图像。 卷积神经网络将更适合于图像分类，但这是一个你已经熟悉的简单例子。 我们将把每个图像视为 28 行 28 像素的序列（因为每个MNIST图像是28×28像素）。 我们将使用 150 个循环神经元的单元，再加上一个全连接层，其中包含连接到上一个时间步的输出的 10 个神经元（每个类一个），然后是一个 softmax 层（见图）。

建模阶段非常简单， 它和我们在之前中建立的 MNIST 分类器几乎是一样的，只是展开的 RNN 替换了隐层。 注意，全连接层连接到状态张量，其仅包含 RNN 的最终状态（即，第 28 个输出）。 另请注意，y是目标类的占位符。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

n_steps = 28
n_inputs = 28
n_neurons = 150
n_outputs = 10

learning_rate = 0.001

X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
y = tf.placeholder(tf.int32, [None])

basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons)
outputs, states = tf.nn.dynamic_rnn(basic_cell, X, dtype=tf.float32)

logits = tf.layers.dense(states, n_outputs)
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y,
                                                          logits=logits)
loss = tf.reduce_mean(xentropy)
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
training_op = optimizer.minimize(loss)
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))

init = tf.global_variables_initializer()

现在让我们加载 MNIST 数据，并按照网络的预期方式将测试数据重塑为[batch_size, n_steps, n_inputs]。 我们之后会关注训练数据的重塑。

1
2
3
4

from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/")
X_test = mnist.test.images.reshape((-1, n_steps, n_inputs))
y_test = mnist.test.labels

现在我们准备训练 RNN 了。 执行阶段与第 10 章中 MNIST 分类器的执行阶段完全相同，不同之处在于我们在将每个训练的批量提供给网络之前要重新调整。

现在我们准备训练 RNN 了。 执行阶段与第 10 章中 MNIST 分类器的执行阶段完全相同，不同之处在于我们在将每个训练的批量提供给网络之前要重新调整。

1
2
3
4
5
6
7
8
9
10
11
12
13

batch_size = 150

with tf.Session() as sess:
    init.run()
    for epoch in range(n_epochs):
        for iteration in range(mnist.train.num_examples // batch_size):
            X_batch, y_batch = mnist.train.next_batch(batch_size)
            X_batch = X_batch.reshape((-1, n_steps, n_inputs))
            sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
        acc_train = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
        acc_test = accuracy.eval(feed_dict={X: X_test, y: y_test})
        print(epoch, "Train accuracy:", acc_train, "Test accuracy:", acc_test)

输出应该是这样的：

我们获得了超过 98% 的准确性 - 不错！ 另外，通过调整超参数，使用 He 初始化初始化 RNN 权重，更长时间训练或添加一些正则化（例如，droupout），你肯定会获得更好的结果。

你可以通过将其构造代码包装在一个变量作用域内（例如，使用variable_scope("rnn", initializer = variance_scaling_initializer())来使用 He 初始化）来为 RNN 指定初始化器。

为预测时间序列而训练

首先，我们来创建一个 RNN。 它将包含 100 个循环神经元，并且我们将在 20 个时间步骤上展开它，因为每个训练实例将是 20 个输入那么长。 每个输入将仅包含一个特征（在该时间的值）。 目标也是 20 个输入的序列，每个输入包含一个值。 代码与之前几乎相同：

一般来说，你将不只有一个输入功能。 例如，如果你试图预测股票价格，则你可能在每个时间步骤都会有许多其他输入功能，例如竞争股票的价格，分析师的评级或可能帮助系统进行预测的任何其他功能。

在每个时间步，我们现在有一个大小为 100 的输出向量。但是我们实际需要的是每个时间步的单个输出值。 最简单的解决方法是将单元包装在OutputProjectionWrapper中。 单元包装器就像一个普通的单元，代理每个方法调用一个底层单元，但是它也增加了一些功能。Out putProjectionWrapper在每个输出之上添加一个完全连接的线性神经元层（即没有任何激活函数）（但不影响单元状态）。 所有这些完全连接的层共享相同（可训练）的权重和偏差项。 结果 RNN 如图所示

装单元是相当容易的。 让我们通过将BasicRNNCell包装到OutputProjectionWrapper中来调整前面的代码：

1
2
3

cell =tf.contrib.rnn.OutputProjectionWrapper(
    tf.contrib.rnn.BasicRNNCell(num_units=n_neurons,activation=tf.nn.relu),
    output_size=n_outputs)

到现在为止还挺好。 现在我们需要定义损失函数。 我们将使用均方误差（MSE），就像我们在之前的回归任务中所做的那样。 接下来，我们将像往常一样创建一个 Adam 优化器，训练操作和变量初始化操作。（省略）

生成 RNN

到现在为止，我们已经训练了一个能够预测未来时刻样本值的模型，正如前文所述，可以用模型来生成新的序列。

为模型提供 长度为n_steps的种子序列, 比如全零序列，然后通过模型预测下一时刻的值；把该预测值添加到种子序列的末尾，用最后面 长度为n_steps的序列做为新的种子序列，做下一次预测，以此类推生成预测序列。

1
2
3
4
5

sequence = [0.] * n_steps
for iteration in range(300):
    X_batch = np.array(sequence[-n_steps:].reshape(1, n_steps, 1)
    y_pred = sess.run(outputs, feed_dict={X: X_batch}
    sequence.append(y_pred[0, -1, 0]

LSTM 单元

在训练长序列的 RNN 模型时，那么就需要把 RNN 在时间维度上展开成很深的神经网络。正如任何深度神经网络一样，其面临着梯度消失/爆炸的问题，使训练无法终止或收敛。很多之前讨论过的缓解这种问题的技巧都可以应用在深度展开的 RNN 网络：好的参数初始化方式，非饱和的激活函数（如 ReLU），批量规范化（Batch Normalization）， 梯度截断（Gradient Clipping），更快的优化器。

即便如此， RNN 在处理适中的长序列（如 100 输入序列）也在训练时表现的很慢。最简单和常见的方法解决训练时长问题就是在训练阶段仅仅展开限定时间步长的 RNN 网络，一种称为截断时间反向传播的算法。

在长的时间训练过程中，第二个要面临的问题时第一个输入的记忆会在长时间运行的 RNN 网络中逐渐淡去。 那么在一定时间后，第一个输入实际上会在 RNN 的状态中消失于无形。 为了解决其中的问题，各种能够携带长时记忆的神经单元的变体被提出。这些变体是有效的，往往基本形式的神经单元就不怎么被使用了。

首先了解一下最流行的一种长时记忆神经单元：长短时记忆神经单元 LSTM。 可以看下面这篇文章

理解LSTM网络

注：LSTM和GRU单元是近年来RNN成功背后的主要原因之一，特别实在自然语言的应用

认识卷积神经网络

全连接神经网络之所以不太适合图像识别任务，主要有三个方面的问题：

• 参数数量太多，一个输入1000×1000像素的图片有100万个神经元（一个像素点代表一个神经元）
• 没有利用像素之间的位置信息
• 网络层数限制，网络层数越多，其表达能力越强，但是通过梯度下降方法训练深度全连接神经网络很困难，因为全连接神经网络的梯度很难传递超过三层。

局部感受野（local receptive fields）

在之前的全连接神经网络中，一个样例的输入被转换为一个一维向量。但在一个卷积网络中，把输入看作是一个按照28×28排列的正方形，或者当有颜色通道的时候，比如28x28x3，就是宽高都是28，且有3个颜色通道。比如下图就代表了一个输入

然后，我们通常把输入像素连接到一个隐藏层的神经元，但和全连接神经网络那样每个输入都连接一个隐藏层神经元不同的是，这里我们只是把输入图像进行局部的连接。

如此不断地重复，构建起第一个隐藏层。注意如果我们有一个28×28的输入图像，5×5的局部感受野，那么隐藏层中就会有24×24个神经元。这是因为在抵达抵达最右边或最底部的输入图像之前，我们只能把局部感受野向右或向下移动23个神经元。

如上图所示，把图中间的那个看作是可以“滑动的窗口”，他的作用是和输入相应的“感受域”下的像素做运算得到新的值。这个运算就是“卷积”运算了。图上面有详细的运算过程。实际上就是每个相应元素的值相乘，然后把得到的都加起来。这个窗口的本质是其中的数字和一个偏置构成的，通常就把这个窗口(Convolution kernel)叫做滤波器或者卷积核（相当于是全连接层里面要求的隐藏权重，它代表识别某个特征）。 这个“窗口”是可以滑动的，每次的滑动步长可以人为指定 。

池化(Pooling)

它的作用是逐渐降低数据体的空间尺寸，这样的话就能减少网络中参数的数量，使得计算资源耗费变少，也能有效控制过拟合。最常见的形式是汇聚层使用尺寸2x2的滤波器，以步长为2来对每个深度切片进行降采样，将其中75%的激活信息都丢掉。每个MAX操作是从4个数字中取最大值（也就是在深度切片中某个2x2的区域）。深度保持不变。

Pooling的方法很多，最常用的是Max Pooling。 此外，还有平均池化（average pooling）和L2-norm池化。

卷积神经网络的层

首先，让我们对卷积神经网络有一个感性的认识，下图就是一个卷积神经网络的示意图：

如上图所示，一个神经网络由若干卷积层（CONV）、Pooling层（POOL）、全连接层（FC）组成。你可以构建各种不同的卷积神经网络，它的常用架构模式为：

也就是N个卷积层叠加，然后叠加一个Pooling层（可选），重复这个结构M次，最后叠加K个全连接层。

对于上图来说，该卷积神经网络的架构为：

也就是N=1,M=2,K=2

我们看到输入层的宽度和高度对应于输入图像的宽度和高度，而他的深度为1。接着第一个卷积层对这幅图像进行了卷积操作，得到了三个Feature Map。实际上这个卷积层包含三个Filter（卷积核，是隐藏不显示图上的），也就是三套参数，每个Filter都可以把原始输入图像卷积得到一个Feature Map，三个Filter就可以得到三个Feature Map。至于一个卷积层可以有多少个Filter，那是可以自由设定的。也就是说，卷积层的Filter个数也是一个超参数。我们可以把Feature Map可以看做是通过卷积变换提取到的图像特征，三个Filter就对原始图像提取出三组不同的特征，也就是得到了三个Feature Map，也称做三个通道(channel)。

在第一个卷积层之后，Pooling层对三个Feature Map做了下采样，得到了三个更小的Feature Map。接着，是第二个卷积层，它有5个Filter。每个Fitler都把前面下采样之后的3个Feature Map卷积在一起（每个Fitlter与输入有相同的深度，然后对应相乘后总相加），得到一个新的Feature Map。这样，5个Filter就得到了5个Feature Map。接着，是第二个Pooling，继续对5个Feature Map进行下采样，得到了5个更小的Feature Map。

最后两层是全连接层。第一个全连接层的每个神经元，和上一层5个Feature Map中的每个神经元相连，第二个全连接层(也就是输出层)的每个神经元，则和第一个全连接层的每个神经元相连，这样得到了整个网络的输出。

至此，我们对卷积神经网络有了最基本的感性认识。接下来，我们将介绍卷积神经网络中各种层的计算和训练。

卷积层

卷积层的参数是一些可学习的滤波器（卷积核，隐藏不显示，相当于全连接层的隐藏权重）构成，滤波器的宽度和高度一般不大，深度与其输入数据保持一致。见下图：

要点：卷积层有一个或多个滤波器（卷积核）构成，每个卷积核宽度和高度（这里为5×5）一般不大，深度（这里为3）与其输入数据保持一致。这里有6个不同的卷积核，得到的6个不同的activation map分别表示诸如边缘特征、形状特征等特征图，将这些activation map映射在深度方向上层叠起来就生成了输出数据。所以在用了6个过滤器（卷积层）之后，我们可以得到28×28×6的激活图。

卷积层输出值的计算

我们使用一个简单的例子来讲述如何计算卷积，然后，抽象出卷积层的一些重要概念和计算方法。

假设有一个5×5的图像，使用一个3×3的滤波器进行卷积，想得到3×3的Feature Map，如下所示：

为了清楚地描述卷积的计算过程，我们首先对图像的每个像素进行编号，用$x_{i,j}$表示图像的第i行第j列元素，对filter的每个权重进行编号，用$w_{m,n}$表示第m行第n列权重，用$w_b$表示filter的偏置项；对Feature Map的每个元素进行编号，用$a_{i,j}$表示Feature Map的第i行第j列元素；用f表示激活函数（此处使用Relu函数作为激活函数）。然后使用下列公式计算卷积：

例如，对于Feature Map的左上角元素$a_{0,0}$来说，其卷积计算方法为：

按照这个公式可以依次计算出Feature Map中所有的值，下面的动画显示了整个Feature Map的计算过程：

填充和步幅

假设输入形状的$n_h\times n_w$，卷积核窗口形状是$k_h\times k_w$，那么输出的形状将会是

所以卷积层的输出形状由输⼊形状和卷积核窗口形状决定。这里我们将介绍卷积层的两个超参数，填充和步幅。它们可以对给定形状的输⼊和卷积核改变输出形状。

填充（padding）是指在输入和宽的两侧填充元素（通常是0元素）。下图表示在原输入高的宽的两侧分别添加了值为0的元素，使得高和宽从3变成了5，并导致输出的高和宽由2增加到4.

卷积窗口从输⼊数组的最左上⽅开始，按从左往右、从上往下的顺序，依次在输⼊数组上滑动。我们将每次滑动的⾏数和列数称为步幅（stride）

上面的计算过程中，步幅（stride）为1。当然步幅可以设为大于1的数。例如，当步幅为2时，Feature Map计算如下：

多输入通道

到此我们讲了深度为1的卷积层的计算方法，如果深度大于1怎么计算呢？其实也是类似的。 下图展⽰了含2个输⼊通道的⼆维互相关计算的例⼦。在每个通道上，⼆维输⼊数组与⼆维核数组做互相关运算，再按通道相加即得到输出。图中阴影部分为第⼀个输出元及其计算所使⽤的输⼊和核数组元素：

动画演示

内存需求

CNN 的另一个问题是卷积层需要大量的 RAM，特别是在训练期间，因为反向传播需要在正向传递期间计算的所有中间值。

如果由于内存不足错误导致训练崩溃，则可以尝试减少小批量大小。 或者，您可以尝试使用步幅降低维度，或者删除几个图层。 或者你可以尝试使用 16 位浮点数而不是 32 位浮点数。 或者你可以在多个设备上分发 CNN。

CNN 架构

典型的 CNN 体系结构有一些卷积层（每一个通常跟着一个 ReLU 层），然后是一个池化层，然后是另外几个卷积层（+ ReLU），然后是另一个池化层，等等。 随着网络的进展，图像变得越来越小，但是由于卷积层的缘故，图像通常也会越来越深（即更多的特征映射）。 在堆栈的顶部，添加由几个全连接层（+ ReLU）组成的常规前馈神经网络，并且最终层输出预测（例如，输出估计类别概率的 softmax 层）。

一个常见的错误是使用太大的卷积核。 通常可以通过将两个3×3内核堆叠在一起来获得与9×9内核相同的效果，计算量更少。

多年来，这种基础架构的变体已经被开发出来，导致了该领域的惊人进步。这里就不展开讲了，大家感兴趣可以去找相关的论文和资料深入了解这些流行的CNN架构。

LeNet-5

LeNet-5 架构也许是最广为人知的 CNN 架构。 如前所述，它是由 Yann LeCun 于 1998 年创建的，广泛用于手写数字识别（MNIST）。

AlexNet

AlexNet CNN 架构赢得了 2012 年的 ImageNet ILSVRC 挑战赛：它达到了 17% 的 top-5 的错误率，而第二名错误率只有 26%！ 它由 Alex Krizhevsky（因此而得名），Ilya Sutskever 和 Geoffrey Hinton 开发。 它与 LeNet-5 非常相似，只是更大更深，它是第一个将卷积层直接堆叠在一起，而不是在每个卷积层顶部堆叠一个池化层。

VGG

它名字来源于论⽂作者所在的实验室Visual Geometry Group。VGG提出了可以通过重复使⽤简单的基础块来构建深度模型的思路.

VGG块的组成规律是：连续使⽤数个相同的填充为1、窗口形状为3 × 3的卷积层后接上⼀个步幅为2、窗口形状为2 × 2的最⼤池化层。卷积层保持输⼊的⾼和宽不变，而池化层则对其减半。VGG⽹络同Alex Net和Le Net⼀样，VGG⽹络由卷积层模块后接全连接层模块构成。。全连接模块则跟Alex Net中的⼀样。

GoogLeNet

GoogLeNet 架构是由 Christian Szegedy 等人开发的。 来自 Google Research，通过低于 7% 的 top-5 错误率，赢得了 ILSVRC 2014 的挑战赛。 这个伟大的表现很大程度上因为它比以前的 CNN 网络更深。 这是通过称为初始模块（inception modules）的子网络实现的，这使得 GoogLeNet 比以前的架构更有效地使用参数：实际上，GoogLeNet 的参数比 AlexNet 少了 10 倍（约 600 万而不是 6000 万）。

ResNet

最后是，2015 年 ILSVRC 挑战赛的赢家 Kaiming He 等人开发的 Residual Network（或 ResNet），该网络的 top-5 误率低到惊人的 3.6%，它使用了一个非常深的 CNN，由 152 层组成。 能够训练如此深的网络的关键是使用跳过连接（skip connection，也称为快捷连接）：一个层的输入信号也被添加到位于下一层的输出。 让我们看看为什么这是有用的。

当训练一个神经网络时，目标是使其模拟一个目标函数h(x)。 如果将输入x添加到网络的输出中（即添加跳过连接），那么网络将被迫模拟f(x)= h(x) - x而不是h(x)。 这被称为残留学习

当你初始化一个普通的神经网络时，它的权重接近于零，所以网络只输出接近零的值。 如果添加跳过连接，则生成的网络只输出其输入的副本; 换句话说，它最初对身份函数进行建模。 如果目标函数与身份函数非常接近（常常是这种情况），这将大大加快训练速度。 由于跳过连接，信号可以很容易地通过整个网络。 深度剩余网络可以看作是一堆剩余单位，其中每个剩余单位是一个有跳过连接的小型神经网络。

现在让我们看看 ResNet 的架构（见下图）。 这实际上是令人惊讶的简单。 它的开始和结束与GoogLeNet完全一样（除了没有 dropout 层），而在两者之间只是一堆很简单的残余单位。 每个残差单元由两个卷积层组成，使用3×3的内核和保存空间维度（步幅 1，SAME填充），批量归一化（BN）和 ReLU 激活。

正如你所看到的，这个领域正在迅速发展，每年都会有各种各样的架构出现。 一个明显的趋势是 CNN 越来越深入。 他们也越来越轻量，需要越来越少的参数。 目前，ResNet 架构既是最强大的，也是最简单的，所以它现在应该是你应该使用的 。

Res Net中的跨层连接设计引申出了数个后续⼯作，稠密连接⽹络（Dense Net）是其中一个，Dense Net的主要构建模块是稠密块（dense block）和过渡层（transition layer）。前者定义了输⼊和输出是如何连结的，后者则⽤来控制通道数，使之不过⼤。

还有其他一些架构可供您参考，特别是 VGGNet（2014 年 ILSVRC 挑战赛的亚军）和 Inception-v4（将 GooLeNet 和 ResNet 的思想融合在一起，实现了接近 3% 的 top-5 误差 ImageNet 分类率）。

前面介绍了人工神经网络，并训练了我们的第一个深度神经网络。 但它是一个非常浅的 DNN，只有两个隐藏层。 如果你需要解决非常复杂的问题，例如检测高分辨率图像中的数百种类型的对象，该怎么办？ 你可能需要训练更深的 DNN，也许有 10 层，每层包含数百个神经元，通过数十万个连接来连接。 这会相当困难

• 首先，你将面临棘手的梯度消失问题（或相关的梯度爆炸问题），这会影响深度神经网络，并使较低层难以训练。
• 其次，对于如此庞大的网络，训练将非常缓慢。
• 第三，具有数百万参数的模型将会有严重的过拟合训练集的风险。

在本章中，我们将从解释梯度消失问题开始，并探讨解决这个问题的一些最流行的解决方案。 接下来我们将看看各种优化器，它们可以加速大型模型的训练。 最后，我们将浏览一些流行的大型神经网络正则化技术。 使用这些工具，你将能够训练非常深的网络：欢迎来到深度学习的世界！

梯度消失/爆炸问题

反向传播算法的工作原理是从输出层到输入层，传播误差的梯度。 一旦该算法已经计算了网络中每个参数的损失函数的梯度，它就使用这些梯度来用梯度下降步骤来更新每个参数。

不幸的是，梯度往往变得越来越小，随着算法进展到较低层。 结果，梯度下降更新使得低层连接权重实际上保持不变，并且训练永远不会收敛到良好的解决方案。 这被称为梯度消失问题。 在某些情况下，可能会发生相反的情况：梯度可能变得越来越大，许多层得到了非常大的权重更新，算法发散。这是梯度爆炸的问题，在循环神经网络中最为常见 。

Xavier初始化和 He 初始化

虽然这种不幸的行为已经经过了相当长的一段时间的实验观察 但直到 2010 年左右，人们才有了明显的进步。 Xavier Glorot 和 Yoshua Bengio 发表的题为《Understanding the Difficulty of Training Deep Feedforward Neural Networks》的论文分析了一些疑问，包括流行的 sigmoid 激活函数和当时最受欢迎的默认权重参数初始化技术的组合，即随机初始化时使用平均值为 0，标准差为 1 的正态分布 。

简而言之，他们表明，用这个激活函数和这个初始化方案，每层输出的方差远大于其输入的方差。网络正向，每层的方差持续增加，直到激活函数在顶层饱和。这实际上是因为logistic函数的平均值为 0.5 而不是 0（双曲正切函数的平均值为 0，表现略好于深层网络中的logistic函数） 。看一下logistic 激活函数，可以看到当输入变大（负或正）时，函数饱和在 0 或 1，导数非常接近 0。因此，当反向传播开始时， 它几乎没有梯度通过网络传播回来，而且由于反向传播通过顶层向下传递，所以存在的小梯度不断地被稀释，因此较低层确实没有任何东西可用。

Glorot 和 Bengio 在他们的论文中提出了一种显著缓解这个问题的方法。 我们需要信号在两个方向上正确地流动：在进行预测时是正向的，在反向传播梯度时是反向的。 我们不希望信号消失，也不希望它爆炸并饱和。 为了使信号正确流动，作者认为，我们需要每层输出的方差等于其输入的方差。

实际上不可能保证两者都是一样的，除非这个层具有相同数量的输入和输出连接，但是他们提出了一个很好的折衷办法，在实践中证明这个折中办法非常好：随机初始化连接权重必须如下面公式所描述的那样。其中n_inputs和n_outputs是权重正在被初始化的层（也称为扇入和扇出）的输入和输出连接的数量。 这种初始化策略通常被称为Xavier初始化（在作者的名字之后） 。很多初始化策略也都是为了保持每层的分布不变 ，这样利于传递信息 。

使用 Xavier 初始化策略可以大大加快训练速度，这是导致深度学习目前取得成功的技巧之一。 最近的一些论文针对不同的激活函数提供了类似的策略，如下表所示。 ReLU 激活函数（及其变体，包括简称 ELU 激活）的初始化策略有时称为 He 初始化（在其作者的姓氏之后）。

非饱和激活函数

激活函数在深度神经网络中表现得更好，特别是 ReLU 激活函数，主要是因为它对正值不会饱和（也因为它的计算速度很快）。

不幸的是，ReLU激活功能并不完美。 它有一个被称为 “ReLU 死区” 的问题：在训练过程中，一些神经元有效地死亡，意味着它们停止输出 0 以外的任何东西。在某些情况下，你可能会发现你网络的一半神经元已经死亡，特别是如果你使用大学习率。 在训练期间，如果神经元的权重得到更新，使得神经元输入的加权和为负，则它将开始输出 0 。当这种情况发生时，由于当输入为负时，ReLU函数的梯度为0，神经元不可能恢复生机。

为了解决这个问题，你可能需要使用 ReLU 函数的一个变体，比如 leaky ReLU。这个函数定义为LeakyReLUα(z)= max(αz，z) 。超参数α定义了函数“leaks”的程度：它是z < 0时函数的斜率，通常设置为 0.01。这个小斜坡确保 leaky ReLU 永不死亡；他们可能会长期昏迷，但他们有机会最终醒来。 事实上，设定α= 0.2（巨大 leak）似乎导致比α= 0.01（小 leak）更好的性能。

最后，Djork-Arné Clevert 等人在 2015 年的一篇论文中提出了一种称为指数线性单元（exponential linear unit，ELU）的新的激活函数，在他们的实验中表现优于所有的 ReLU 变体：训练时间减少，神经网络在测试集上表现的更好，如下所示。

它看起来很像 ReLU 函数，但有一些区别，主要区别在于：

• 首先它在z < 0时取负值，这使得该单元的平均输出接近于 0。这有助于减轻梯度消失问题，如前所述。 超参数α定义为当z是一个大的负数时，ELU 函数接近的值。它通常设置为 1，但是如果你愿意，你可以像调整其他超参数一样调整它。
• 其次，它对z < 0有一个非零的梯度，避免了神经元死亡的问题。
• 第三，函数在任何地方都是平滑的，包括z = 0左右，这有助于加速梯度下降，因为它不会弹回z = 0的左侧和右侧。

ELU 激活函数的主要缺点是计算速度慢于 ReLU 及其变体（由于使用指数函数），但是在训练过程中，这是通过更快的收敛速度来补偿的。 然而，在测试时间，ELU 网络将比 ReLU 网络慢。

那么你应该使用哪个激活函数来处理深层神经网络的隐藏层？ 虽然你的里程会有所不同，一般 ELU > leaky ReLU（及其变体）> ReLU > tanh > sigmoid。 如果您关心运行时性能，那么您可能喜欢 leaky ReLU超过ELU。

批量标准化

尽管使用 He初始化和 ELU（或任何 ReLU 变体）可以显著减少训练开始阶段的梯度消失/爆炸问题，但不保证在训练期间问题不会回来。

在 2015 年的一篇论文中，Sergey Ioffe 和 Christian Szegedy 提出了一种称为批量标准化（Batch Normalization，BN）的技术来解决梯度消失/爆炸问题，每层输入的分布在训练期间改变的问题，更普遍的问题是当前一层的参数改变，每层输入的分布会在训练过程中发生变化（他们称之为内部协变量偏移问题）。

该技术包括在每层的激活函数之前在模型中添加操作，简单地对输入进行zero-centering和规范化，然后每层使用两个新参数（一个用于尺度变换，另一个用于偏移）对结果进行尺度变换和偏移。 换句话说，这个操作可以让模型学习到每层输入值的最佳尺度,均值。为了对输入进行归零和归一化，算法需要估计输入的均值和标准差。 它通过评估当前小批量输入的均值和标准差（因此命名为“批量标准化”）来实现。

在测试时，没有小批量计算经验均值和标准差，所以您只需使用整个训练集的均值和标准差。 这些通常在训练期间使用移动平均值进行有效计算。 因此，总的来说，每个批次标准化的层次都学习了四个参数：γ（标度），β（偏移），μ（平均值）和σ（标准差）

作者证明，这项技术大大改善了他们试验的所有深度神经网络。梯度消失问题大大减少了，他们可以使用饱和激活函数，如 tanh 甚至 sigmoid 激活函数。网络对权重初始化也不那么敏感。他们能够使用更大的学习率，显著加快了学习过程。 由于每层所需的额外计算，神经网络的预测速度较慢。 所以，如果你需要预测闪电般快速，你可能想要检查普通ELU + He初始化执行之前如何执行批量标准化。您可能会发现，训练起初相当缓慢，而渐变下降正在寻找每层的最佳尺度和偏移量，但一旦找到合理的好值，它就会加速。

当然，如果你训练的时间越长，准确性就越好，但是由于这样一个浅的网络，批量范数和 ELU 不太可能产生非常积极的影响：它们大部分都是为了更深的网络而发光。

批量标准化和初始化权重参数的意义差不多，更深的理解可以看这篇 批量标准化

梯度裁剪

减少梯度爆炸问题的一种常用技术是在反向传播过程中简单地剪切梯度，使它们不超过某个阈值（这对于递归神经网络是非常有用的）。 这就是所谓的梯度裁剪。一般来说，人们更喜欢批量标准化，但了解梯度裁剪以及如何实现它仍然是有用的。

复用预训练层

从零开始训练一个非常大的 DNN 通常不是一个好主意，相反，您应该总是尝试找到一个现有的神经网络来完成与您正在尝试解决的任务类似的任务，然后复用这个网络的较低层：这就是所谓的迁移学习。这不仅会大大加快训练速度，还将需要更少的训练数据。 一般包括三个步骤

1、冻结较低层：在训练过程中变量不会发生变化（通常称为冻结层）。

2、缓存冻结层：由于冻结层不会改变，因此可以为每个训练实例缓存最上面的冻结层的输出。 由于训练贯穿整个数据集很多次，这将给你一个巨大的速度提升

3、调整，删除或替换较高层：对于新任务来说最有用的高层特征可能与对原始任务最有用的高层特征明显不同。 你需要找到正确的层数来复用。 一般拥有的训练数据越多，您可以解冻的层数就越多。

Model Zoos

你在哪里可以找到一个类似于你想要解决的任务训练的神经网络？ 首先看看显然是在你自己的模型目录。 这是保存所有模型并组织它们的一个很好的理由，以便您以后可以轻松地检索它们。 另一个选择是在模型动物园中搜索。 许多人为了各种不同的任务而训练机器学习模型，并且善意地向公众发布预训练模型。

TensorFlow 在 https://github.com/tensorflow/models 中有自己的模型动物园。 特别是，它包含了大多数最先进的图像分类网络，如 VGG，Inception 和 ResNet（参见第 13 章，检查model/slim目录），包括代码，预训练模型和 工具来下载流行的图像数据集。

另一个流行的模型动物园是 Caffe 模型动物园。 它还包含许多在各种数据集（例如，ImageNet，Places 数据库，CIFAR10 等）上训练的计算机视觉模型（例如，LeNet，AlexNet，ZFNet，GoogLeNet，VGGNet，开始）。 Saumitro Dasgupta 写了一个转换器，可以在 https://github.com/ethereon/caffetensorflow。

更快的优化器

练一个非常大的深度神经网络可能会非常缓慢。 到目前为止，我们已经看到了四种加速训练的方法（并且达到更好的解决方案）：对连接权重应用良好的初始化策略，使用良好的激活函数，使用批量规范化以及重用预训练网络的部分。 另一个巨大的速度提升来自使用比普通渐变下降优化器更快的优化器。 在本节中，我们将介绍最流行的：动量优化，Nesterov 加速梯度，AdaGrad，RMSProp，最后是 Adam 优化。

剧透：本节的结论是，您几乎总是应该使用Adam_optimization，所以如果您不关心它是如何工作的，只需使用AdamOptimizer替换您的GradientDescentOptimizer，然后跳到下一节！ 只需要这么小的改动，训练通常会快几倍。 但是，Adam 优化确实有三个可以调整的超参数（加上学习率）。 默认值通常工作的不错，但如果您需要调整它们，知道他们怎么实现的可能会有帮助。

理解这些优化器可以看这篇 神经网络的优化方法

训练稀疏模型

上面所有刚刚提出的优化算法都会产生密集的模型，这意味着大多数参数都是非零的。 如果你在运行时需要一个非常快速的模型，或者如果你需要它占用较少的内存，你可能更喜欢用一个稀疏模型优化器来代替。

这时可以使用FTRL 优化器，一种由尤里·涅斯捷罗夫（Yurii Nesterov）提出的技术。 当与 l1 正则化一起使用时，这种技术通常导致非常稀疏的模型。

学习率调整

自适应下降的学习速率会更好。有三种流行的方法：

• 性能调度：每 N 步测量验证误差（就像提前停止一样），当误差下降时，将学习率降低一个因子λ。
• 指数调度：将学习率设置为迭代次数t的函数$\eta(t)=\eta_0\cdot10^{-t/r}$： 这很好，但它需要调整初始速率η0和总迭代次数r。 学习率将由每r步下降 10 倍。
• 幂调度：设学习率为$\eta(t)=\eta_0(1+t/r)^{-c}$。 超参数c通常被设置为 1。这与指数调度类似，但是学习率下降要慢得多。

根据Andrew Senior 等2013年的论文。 比较了使用动量优化训练深度神经网络进行语音识别时一些最流行的学习率调整的性能。 作者得出结论：在这种情况下，性能调度和指数调度都表现良好，但他们更喜欢指数调度，因为它实现起来比较简单，容易调整，收敛速度略快于最佳解决方案 。

通过正则化避免过拟合

1、早起停止法

2、L1和L2正则化：注意不需要对bias正则，只对权重

3、Dropout

深度神经网络最流行的正则化技术可以说是 dropout。 它由 GE Hinton 于 2012 年提出，并在 Nitish Srivastava 等人的论文中进一步详细描述，并且已被证明是非常成功的：即使是最先进的神经网络，仅仅通过增加丢失就可以提高1-2％的准确度。

是一个相当简单的算法：在每个训练步骤中，每个神经元（包括输入神经元，但不包括输出神经元）都有一个暂时“丢弃”的概率p，这意味着在这个训练步骤中它将被完全忽略， 在下一步可能会激活（见下图 ）。 超参数p称为丢失率，通常设为 50%。 训练后，神经元不会再下降。

如果观察到模型过拟合，则可以增加 dropout 率（即，减少keep_prob超参数）。 相反，如果模型欠拟合训练集，则应尝试降低 dropout 率（即增加keep_prob）。 它也可以帮助增加大层的 dropout 率，并减少小层的 dropout 率。

dropout 似乎减缓了收敛速度，但通常会在调整得当时使模型更好。 所以，这通常值得花费额外的时间和精力。

Dropconnect是dropout的变体，其中单个连接随机丢弃而不是整个神经元。 一般而言，dropout表现会更好。

最大范数正则化

另一种在神经网络中非常流行的正则化技术被称为最大范数正则化：对于每个神经元，它约束输入连接的权重w，使得$\Vert w\Vert_2 \leq r$，其中r是最大范数超参数，$\Vert \cdot \Vert$是 L2 范数。

我们通常通过在每个训练步骤之后计算 $\Vert w\Vert_2$来实现这个约束，并且如果需要的话可以剪切W ，即$w\leftarrow w\frac{r}{\Vert w\Vert_2}$。

减少r增加了正则化的数量(经常剪切W)，并有助于减少过拟合。 最大范数正则化还可以帮助减轻梯度消失/爆炸问题（如果您不使用批量标准化）。

数据增强

最后一个正则化技术，数据增强，包括从现有的训练实例中产生新的训练实例，人为地增加了训练集的大小。 这将减少过拟合，使之成为正则化技术。 诀窍是生成逼真的训练实例;

例如，如果您的模型是为了分类蘑菇图片，您可以稍微移动，旋转和调整训练集中的每个图片的大小，并将结果图片添加到训练集。 这迫使模型更能容忍图片中蘑菇的位置，方向和大小。 如果您希望模型对光照条件更加宽容，则可以类似地生成具有各种对比度的许多图像。 假设蘑菇是对称的，你也可以水平翻转图片。 通过结合这些转换，可以大大增加训练集的大小。

实践指南

当然，如果你能找到解决类似问题的方法，你应该尝试重用预训练的神经网络的一部分。

这个默认配置可能需要调整：

• 如果你找不到一个好的学习率（收敛速度太慢，所以你增加了训练速度，现在收敛速度很快，但是网络的准确性不是最理想的），那么你可以尝试添加一个学习率调整，如指数衰减。
• 如果你的训练集太小，你可以实现数据增强。
• 如果你需要一个稀疏的模型，你可以添加 l1 正则化混合（并可以选择在训练后将微小的权重归零）。 如果您需要更稀疏的模型，您可以尝试使用 FTRL 而不是 Adam 优化以及 l1 正则化。
• 如果在运行时需要快速模型，则可能需要删除批量标准化，并可能用 leakyReLU 替换 ELU 激活函数。 有一个稀疏的模型也将有所帮助。

1. 使用 He 初始化随机选择权重，是否可以将所有权重初始化为相同的值？

答：不，所有的权值都应该独立采样;它们的初值不应该相同。如果任意一层的所有神经元都有相同的权值。这就像每层只有一个神经元，而且速度要慢得多。

1. 可以将偏置初始化为 0 吗？

答：可以

1. 说出 ELU 激活功能与 ReLU 相比的三个优点。

答：

• 它可以取负值，所以任意一层神经元的平均输出通常比使用relu激活函数(从不输出负值)时更接近于0。这有助于缓解渐变消失的问题。
• 它总是有一个非零的导数，这避免了神经元死亡的问题。
• 处处平滑，而Relu的斜率在z = 0时突然从0跳到1。这样的骤减使梯度下降效果降低，因为它会在z =0附近反弹.

1. 在哪些情况下，您想要使用以下每个激活函数：ELU，leaky ReLU（及其变体），ReLU，tanh，logistic 以及 softmax？

答：ELU是一个不错的默认选择。如果想要训练速度更快一些可以采用 leaky ReLU（及其变体）

1. dropout 是否会减慢训练？ 它是否会减慢推断（即预测新的实例）？

答：dropout确实会减慢训练速度，总的来说大概是两倍。然而，它没有对推断（预测新的实例）的影响，因为它只在训练期间打开。

神经元

首先我们从最简单的神经网络——神经元讲起，以下即为一个神经元（Neuron）的图示：

我们知道感知机的激活函数是阶跃函数；而当我们说神经元的时，激活函数往往选择sigmoid函数或tanh函数 ,还有Relu函数（效果较好）。如下图所示

可以看出，这个单一神经元的输入输出的映射关系其实就是一个逻辑回归（logistic regression）。

神经网络模型

神经网络模型

所谓神经网络就是将许多神经元联结在一起，这样，一个神经元的输出就可以是另一神经元的输入。例如，下图就是一个简单的神经网络：

这样的神经网络也称之为多层感知机（MLP），MLP 由一个（通过）输入层、一个或多个称为隐藏层的 LTU （单层感知器）组成，一个最终层 LTU 称为输出层。除了输出层之外的每一层包括偏置神经元，并且全连接到下一层。当人工神经网络有两个或多个隐含层时，称为深度神经网络（DNN）。

BP反向传播

反向传播指的是计算神经⽹络参数梯度的⽅法。总的来说，反向传播依据微积分中的链式法则，沿着从输出层到输⼊层的顺序，依次计算并存储⽬标函数有关神经⽹络各层的中间变量以及参数的梯度。

上图依次为利用dE/dx6求出第一个dE/dw; 利用分量的点对点继续求dE/dw; 利用求和来下一个dE/dy2 ;(这里的所以x,y总输入输出都是知道的)

• dE/dw是有上下夹层dE/dx与上面一层的y求出的
• dE/dy是由上面一层全连接的wij 与其连接的dE/dx求出的

dE/dy2 = dE/dx4, w24 和 dE/dx5, dw25的求和得到其中，y2=w24*x4,故有dx_j/dy_i = wij

用 TensorFlow 高级 API 训练 MLP

与 TensorFlow 一起训练 MLP 最简单的方法是使用高级 API TF.Learn，这与 sklearn 的 API 非常相似。DNNClassifier可以很容易训练具有任意数量隐层的深度神经网络，而 softmax 输出层输出估计的类概率。例如，下面的代码训练两个隐藏层的 DNN（一个具有 300 个神经元，另一个具有 100 个神经元）和一个具有 10 个神经元的 SOFTMax 输出层进行分类：

1
2
3
4
5

import tensorflow as tf
feature_columns = tf.contrib.learn.infer_real_valued_columns_from_input(X) 
dnn_clf = tf.contrib.learn.DNNClassifier(hidden_units=[300, 100], n_classes=10,
                                         feature_columns=feature_columns) 
dnn_clf.fit(x=X, y=y, batch_size=50, steps=40000)

如果你在 MNIST 数据集上运行这个代码（在缩放它之后，例如，通过使用 skLearn 的StandardScaler），你实际上可以得到一个在测试集上达到 98.1% 以上精度的模型！

1

>>> from sklearn.metrics import accuracy_score >>> y_pred = list(dnn_clf.predict(X_test)) >>> accuracy_score(y_test, y_pred) 0.98180000000000001

TF.Learn 学习库也为评估模型提供了一些方便的功能：

1

>>> dnn_clf.evaluate(X_test, y_test) {'accuracy': 0.98180002, 'global_step': 40000, 'loss': 0.073678359}

使用普通 TensorFlow 训练 DNN

如果您想要更好地控制网络架构，您可能更喜欢使用 TensorFlow 的较低级别的 Python API。 在本节中，我们将使用与之前的 API 相同的模型，我们将实施 Minibatch 梯度下降来在 MNIST 数据集上进行训练。 第一步是建设阶段，构建 TensorFlow 图。 第二步是执行阶段，您实际运行计算图谱来训练模型。

构造阶段

开始吧。 首先我们需要导入tensorflow库。 然后我们必须指定输入和输出的数量，并设置每个层中隐藏的神经元数量：

1

import tensorflow as tfn_inputs = 28*28 # MNISTn_hidden1 = 300n_hidden2 = 100n_outputs = 10

接下来，可以使用占位符节点来表示训练数据和目标。X的形状仅有部分被定义。 我们知道它将是一个 2D 张量（即一个矩阵），沿着第一个维度的实例和第二个维度的特征，我们知道特征的数量将是28×28（每像素一个特征） 但是我们不知道每个训练批次将包含多少个实例。 所以X的形状是(None, n_inputs)。 同样，我们知道y将是一个 1D 张量，每个实例有一个入口，但是我们再次不知道在这一点上训练批次的大小，所以形状(None)。

1

X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")y = tf.placeholder(tf.int64, shape=(None), name="y")

现在让我们创建一个实际的神经网络。 占位符X将作为输入层; 在执行阶段，它将一次更换一个训练批次（注意训练批中的所有实例将由神经网络同时处理）。 现在您需要创建两个隐藏层和输出层。 两个隐藏的层几乎相同：它们只是它们所连接的输入和它们包含的神经元的数量不同。 输出层也非常相似，但它使用 softmax 激活函数而不是 ReLU 激活函数。 所以让我们创建一个neuron_layer()函数，我们将一次创建一个图层。 它将需要参数来指定输入，神经元数量，激活函数和图层的名称：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

def neuron_layer(X, n_neurons, name, activation=None):
    with tf.name_scope(name):
        n_inputs = int(X.get_shape()[1])
        stddev = 2 / np.sqrt(n_inputs)
        init = tf.truncated_normal((n_inputs, n_neurons), stddev=stddev)
        W = tf.Variable(init, name="weights") # 使用满足分布概率来更好第初始化W权重
        b = tf.Variable(tf.zeros([n_neurons]), name="biases")
        # multiply这个函数实现的是元素级别的相乘，也就是两个相乘的数元素各自相乘，而不是矩阵乘法
        # tf.matmul才算矩阵乘法，注意区别
        z = tf.matmul(X, W) + b 
        if activation == "relu":
            return tf.nn.relu(z)
        else:
            return z

我们逐行浏览这个代码：

1. 首先，我们使用名称范围来创建每层的名称：它将包含该神经元层的所有计算节点。 这是可选的，但如果节点组织良好，则 TensorBoard 图形将会更加出色。
2. 接下来，我们通过查找输入矩阵的形状并获得第二个维度的大小来获得输入数量（第一个维度用于实例数量）。
3. 接下来的三行创建一个保存权重矩阵的W变量。 它将是包含每个输入和每个神经元之间的所有连接权重的2D张量；因此，它的形状将是(n_inputs, n_neurons)。它将被随机初始化，使用具有标准差为2/√n的截断的正态（高斯）分布(使用截断的正态分布而不是常规正态分布确保不会有任何大的权重，这可能会减慢训练。).使用这个特定的标准差有助于算法的收敛速度更快（我们将在后面进一步讨论这一点），这是对神经网络的微小调整之一，对它们的效率产生了巨大的影响）。 重要的是为所有隐藏层随机初始化连接权重，以避免梯度下降算法无法中断的任何对称性。（例如，如果将所有权重设置为 0，则所有神经元将输出 0，并且给定隐藏层中的所有神经元的误差梯度将相同。 然后，梯度下降步骤将在每个层中以相同的方式更新所有权重，因此它们将保持相等。 换句话说，尽管每层有数百个神经元，你的模型就像每层只有一个神经元一样。）
4. 下一行创建一个偏差的b变量，初始化为 0（在这种情况下无对称问题），每个神经元有一个偏置参数。
5. 然后我们创建一个子图来计算z = X·W + b。 该向量化实现将有效地计算输入的加权和加上层中每个神经元的偏置，对于批次中的所有实例，仅需一次.
6. 最后，如果激活参数设置为relu，则代码返回relu(z)（即max(0,z)），否则它只返回z。

好了，现在你有一个很好的函数来创建一个神经元层。 让我们用它来创建深层神经网络！ 第一个隐藏层以X为输入。 第二个将第一个隐藏层的输出作为其输入。 最后，输出层将第二个隐藏层的输出作为其输入。

1
2
3
4

with tf.name_scope("dnn"):
        hidden1 = neuron_layer(X, n_hidden1, "hidden1", activation="relu")
    hidden2 = neuron_layer(hidden1, n_hidden2, "hidden2", activation="relu")
    logits = neuron_layer(hidden2, n_outputs, "outputs")

要注意，logit 是在通过 softmax 激活函数之前神经网络的输出：为了优化，我们稍后将处理 softmax 计算。

正如你所期望的，TensorFlow 有许多方便的功能来创建标准的神经网络层，所以通常不需要像我们刚才那样定义你自己的neuron_layer()函数。 例如，TensorFlow 的tf.layers.dense()函数创建一个完全连接的层，其中所有输入都连接到图层中的所有神经元。 它使用正确的初始化策略来负责创建权重和偏置变量，并且默认情况下不使用激活函数（我们可以使用activate_fn参数来更改它）。 它还支持正则化和归一化参数。 我们来调整上面的代码来使用tf.layers.dense()函数，而不是我们的neuron_layer()函数。 只需导入该功能，并使用以下代码替换之前所有 dnn 构建部分：

1
2
3
4
5
6

with tf.name_scope("dnn"):
    hidden1 = tf.layers.dense(X, n_hidden1, name="hidden1",
                              activation=tf.nn.relu)
    hidden2 = tf.layers.dense(hidden1, n_hidden2, name="hidden2",
                              activation=tf.nn.relu)
    logits = tf.layers.dense(hidden2, n_outputs, name="outputs")

损失函数

现在我们已经有了神经网络模型，我们需要定义我们用来训练的损失函数。 正如我们在之前对 Softmax 回归所做的那样，我们将使用交叉熵。 我们将使用sparse_softmax_cross_entropy_with_logits()：它根据“logit”计算交叉熵（即，在通过 softmax 激活函数之前的网络输出），并且期望以 0 到 -1 数量的整数形式的标签（在我们的例子中，从 0 到 9）。 这将给我们一个包含每个实例的交叉熵的 1D 张量。 然后，我们可以使用 TensorFlow 的reduce_mean()函数来计算所有实例的平均交叉熵。

1
2
3

with tf.name_scope("loss"):
    xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
    loss = tf.reduce_mean(xentropy, name="loss")

该sparse_softmax_cross_entropy_with_logits()函数等同于应用 SOFTMAX 激活函数，然后计算交叉熵，但它更高效，它妥善照顾的边界情况下，比如 logits 等于 0，这就是为什么我们没有较早的应用 SOFTMAX 激活函数。 还有称为softmax_cross_entropy_with_logits()的另一个函数，该函数在标签单热载体的形式（而不是整数 0 至类的数目减 1）。

优化器

我们有神经网络模型，我们有损失函数，现在我们需要定义一个GradientDescentOptimizer来调整模型参数以最小化损失函数。没什么新鲜的; 就像我们之前中所做的那样：

1
2
3
4
5

learning_rate = 0.01

with tf.name_scope("train"):
    optimizer = tf.train.GradientDescentOptimizer(learning_rate)
    training_op = optimizer.minimize(loss)

评估模型性能

建模阶段的最后一个重要步骤是指定如何评估模型。 我们将简单地将精度用作我们的绩效指标。 首先，对于每个实例，通过检查最高 logit 是否对应于目标类别来确定神经网络的预测是否正确。 为此，您可以使用in_top_k()函数。 这返回一个充满布尔值的 1D 张量，因此我们需要将这些布尔值转换为浮点数，然后计算平均值。 这将给我们网络的整体准确性.

1
2
3

with tf.name_scope("eval"):
    correct = tf.nn.in_top_k(logits, y, 1)
    accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))

而且，像往常一样，我们需要创建一个初始化所有变量的节点，我们还将创建一个Saver来将我们训练有素的模型参数保存到磁盘中：

1
2

init = tf.global_variables_initializer()
saver = tf.train.Saver()

建模阶段结束。 这是不到 40 行代码，但相当激烈：我们为输入和目标创建占位符，我们创建了一个构建神经元层的函数，我们用它来创建 DNN，我们定义了损失函数，我们 创建了一个优化器，最后定义了性能指标。 现在到执行阶段。

执行阶段

首先，我们加载 MNIST。 我们可以像之前的章节那样使用 ScikitLearn，但是 TensorFlow 提供了自己的助手来获取数据，将其缩放（0 到 1 之间），将它洗牌，并提供一个简单的功能来一次加载一个小批量：

1
2
3
4

from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/")
n_epochs = 10001  # 迭代次数
batch_size = 50   # 小批量大小

现在我们去训练模型:

1
2
3
4
5
6
7
8
9
10
11

with tf.Session() as sess:
    init.run()
    for epoch in range(n_epochs):
        for iteration in range(mnist.train.num_examples // batch_size): # 每批量一次
            X_batch, y_batch = mnist.train.next_batch(batch_size)
            sess.run(training_op, feed_dict={X: X_batch, y: y_batch}) # 运行计算程序
        acc_train = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
        acc_test = accuracy.eval(feed_dict={X: mnist.test.images, y: mnist.test.labels})
        print(epoch, "Train accuracy:", acc_train, "Test accuracy:", acc_test)

    save_path = saver.save(sess, "./my_model_final.ckpt")

该代码打开一个 TensorFlow 会话，并运行初始化所有变量的init节点。 然后它运行的主要训练循环：在每个时期，通过一些小批次的对应于训练集的大小的代码进行迭代。 每个小批量通过next_batch()方法获取，然后代码简单地运行训练操作，为当前的小批量输入数据和目标提供。 接下来，在每个时期结束时，代码评估最后一个小批量和完整训练集上的模型，并打印出结果。 最后，模型参数保存到磁盘。

使用神经网络进行预测

现在神经网络被训练了，你可以用它进行预测。 为此，您可以重复使用相同的建模阶段，但是更改执行阶段，如下所示：

1
2
3
4
5

with tf.Session() as sess:
    saver.restore(sess, "./my_model_final.ckpt") # or better, use save_path
    X_new_scaled = mnist.test.images[:20]
    Z = logits.eval(feed_dict={X: X_new_scaled})
    y_pred = np.argmax(Z, axis=1)

首先，代码从磁盘加载模型参数。 然后加载一些您想要分类的新图像。 记住应用与训练数据相同的特征缩放（在这种情况下，将其从 0 缩放到 1）。 然后代码评估对数点节点。 如果您想知道所有估计的类概率，则需要将softmax()函数应用于对数，但如果您只想预测一个类，则可以简单地选择具有最高 logit 值的类（使用argmax()函数做的伎俩）。

微调神经网络超参数

神经网络的灵活性也是其主要缺点之一：有很多超参数要进行调整。 不仅可以使用任何可想象的网络拓扑（如何神经元互连），而且即使在简单的 MLP 中，您可以更改层数，每层神经元数，每层使用的激活函数类型，权重初始化逻辑等等。 你怎么知道什么组合的超参数是最适合你的任务？

可以使用具有交叉验证的网格搜索来查找正确的超参数 ，但是由于要调整许多超参数，并且由于在大型数据集上训练神经网络需要很多时间 。像之前讨论过的，使用随机搜索要好得多 ，另一个选择是使用诸如 Oscar 之类的工具，它可以实现更复杂的算法，以帮助您快速找到一组好的超参数.

隐藏层数量

实际上已经表明，只有一个隐藏层的 MLP 可以建模甚至最复杂的功能，只要它具有足够的神经元。 但是他们忽略了这样一个事实：深层网络具有比浅层网络更高的参数效率：他们可以使用比浅网格更少的神经元来建模复杂的函数，使得训练更快。

总而言之，对于许多问题，您可以从一个或两个隐藏层开始。(MNIST 数据集上容易达到 97% 以上的准确度使用两个具有相同总神经元数量的隐藏层 )；对于更复杂的问题，您可以逐渐增加隐藏层的数量，直到您开始覆盖训练集。 但是，我们很少从头开始训练这样的网络：重用预先训练的最先进的网络执行类似任务的部分更为常见。训练将会更快，需要更少的数据 。

每层隐藏层的神经元数量

不幸的是，正如你所看到的，找到完美的神经元数量仍然是黑色的艺术.

一个更简单的方法是选择一个具有比实际需要的更多层次和神经元的模型，然后使用早期停止来防止它过度拟合（以及其他正则化技术，特别是 drop out，我们将在后面）。 这被称为“拉伸裤”的方法：而不是浪费时间寻找完美匹配您的大小的裤子，只需使用大型伸缩裤，缩小到合适的尺寸。

激活函数

在大多数情况下，您可以在隐藏层中使用 ReLU 激活函数（或其中一个变体 ）

对于输出层，softmax 激活函数通常是分类任务的良好选择（当这些类是互斥的时）。 对于回归任务，您完全可以不使用激活函数。

1. 为什么通常使用逻辑斯蒂回归分类器而不是经典感知器（即使用感知器训练算法训练单层的线性阈值单元）？你如何调整感知器使之等同于逻辑回归分类器？

答：经典感知器只有在数据集是线性可分的情况下才会收敛。相比之下，逻辑回归分类器将收敛于一个很好的解决方案，即使数据集不是线性可分的，它会输出类的概率。如果你将感知器的激活函数改为逻辑激活函数(或如果有多个神经元，则为softmax激活函数)，，则等价于逻辑回归分类器。

1. 为什么激活函数是训练第一个 MLP 的关键因素？

答：logistic激活函数是训练第一批MLP的关键因素，因为它是一个复杂的过程导数总是不为零的，所以梯度下降总是可以沿着斜率向下滚动。当激活函数是阶跃函数，梯度下降无法移动，因为根本没有斜率。

1. 假设有一个 MLP 有一个 10 个神经元组成的输入层，接着是一个 50 个神经元的隐藏层，最后一个 3 个神经元输出层。所有人工神经元使用 Relu 激活函数。

• 输入矩阵X的形状是什么？ —— -m × 10，其中m为batch size.
• 隐藏层的权重向量的形状以及它的偏置向量的形状如何？ ——W_h=50 × 10，b_h = 50（一维长度）
• 输出层的权重向量和它的偏置向量的形状是什么？ ——W_o=50 × 3，b_o=3
• 网络的输出矩阵Y是什么形状？ ——Y=m × 3
• 写出计算网络输出矩阵的方程 —$-Y=(X\cdot W_h+b_h)\cdot W_o+b_o$

1. 如果你想把电子邮件分类成垃圾邮件或正常邮件，你需要在输出层中有多少个神经元？在输出层中应该使用什么样的激活函数？如果你想解决 MNIST 问题，你需要多少神经元在输出层，使用什么激活函数？

答：只需要神经系统在输出层中的一个神经元，通常在估计概率时，使用输出层的logistic激活函数。如果你想处理mnist，你需要输出层的10个神经元，你必须替换
logistic函数与softmax激活函数，它可以处理多个分裂，每个类输出一个概率。如果现在想让你的神经网络预测房屋价格，则需要一个输出神经元，不使用任何激活函数
输出层。

基于密度的聚类

密度聚类方法的指导思想是，只要样本点的密度大于某阈值，则将该样本添加到最近的簇中。这类算法能克服基于距离的算法只能发现“类圆”（凸）的聚类的缺点，可发现任意形状的聚类，且对噪声数据不敏感。但计算密度单元的计算复杂度大，需要建立空间索引来降低计算量。

DBSCAN：一种基于高密度连通区域的密度聚类

DBCSAN（Density-Based Spatial Clustering of Applications with Noise）是一个比较有代表性的基于密度的聚类算法。与划分和层次聚类方法不同，它将簇定义为密度相连的点的最大集合，能够把具有足够高密度的区域划分为簇，并可在有“噪声”的数据中发现任意形状的聚类。

基础概念

• 对象的ϵ−领域：给定对象在半径ϵϵ内的区域
• 核心对象：对于给定的数目m，如果一个对象的ϵ−领域至少包含m个对象，则称该对象为核心对象。
• 直接密度可达：给定一个对象集合D，如果p是在q的ϵ−领域内，而q是一个核心对象，我们说对象p从对象q出发时直接密度可达的。

如图ϵ=1 ，m=5， q是一个核心对象，从对象q出发到对象p是直接密度可达的。

• 密度可达：如果存在一个对象链$p_1,p_2,⋅⋅⋅,p_n$，使得$p_1=q$，$p_n=p$，并且对$p_i (1≤i≤n)∈D$，有$p_{i+1}$是从$p_i$关于ϵ和m直接密度可达的，则p是从q密度可达的(也就是中间连接了多个直接密度可达)。注意密度可达不是等价关系，因为它不是对称的。如果$o_1$和$o_2$都是核心对象，则都是密度可达；如果$o_2$是核心对象$o_1$不是，则$o_1$可能是从$o_2$密度可达，反过来就不可以。（需要从核心出发到不核心）

密度相连：如果对象集合D中存在一个对象o，使得对p和q是从o关于ϵ和m密度可达的，那么对象p和q是关于ϵ和m密度相连的。 (存在中间点o，分别到q和p两条路线都是密度可达，则q和p密度相连)。不像密度可达，密度相连是等价的。

算法步骤：

下面这张图来自WIKI，图上有若干个点，其中标出了A、B、C、N这四个点，据此来说明这个算法的步骤：

• 1、首先随机选择A点为算法实施的切入点，我们将ϵϵ设置为图中圆的半径，对象密度个数$m（minPts）$设定为4。这里我们看到，A点的ϵϵ领域包含4个对象（自己也包含在内），大于等于$m(minPts)$，则创建A作为核心对象的新簇，簇内其他点都（暂时）标记为边缘点。
• 2、然后在标记的边缘点中选取一个重复上一步，寻找并合并核心对象直接密度可达的对象。对暂时标记为边缘点反复递归上述算法，直至没有新的点可以更新簇时，算法结束。这样就形成了一个以A为起始的一个聚类，为图中红色的中心点和黄色的边缘点（黄红点都形成簇）
• 3、如果还有Points未处理，再次新产生一个类别来重新启动这个算法过程。遍历所有数据，如果有点既不是边缘点也不是中心点，将其标记为噪音。

初始，给定数据集D中的所有对象都标记为”unvisited”。DBSCAN随机地选择一个未访问的对象p，标记p为”visited”，并检查p是否为核心对象。如果不是，标记p为噪点，否则为p创建一个新的簇C，并且将领域内所有对象都放到候选集合N中（这个集合会慢慢加大）。DBSCAN迭代地把N中不属于其他簇的对象添加C中。在此过程中，对于N中标记为”unvisited”的对象p’ ，标记为”visited”，如果它是核心对象，则将它的领域节点都添加到N中。DBSCAN继续从候选集N中添加到C，直到N的集合为空。此时，簇C完全生成，于是被输出。

从上述算法可知：

• 每个簇至少包含一个核心对象；
• 非核心对象可以是簇的一部分，构成了簇的边缘（edge）；
• 包含过少对象的簇被认为是噪声；

DBSCAN的主要优点有：

　　1） 可以对任意形状的稠密数据集进行聚类，相对的，K-Means之类的聚类算法一般只适用于凸数据集。

　　2） 可以在聚类的同时发现异常点，对数据集中的异常点不敏感。

　　3） 聚类结果没有偏倚，相对的，K-Means之类的聚类算法初始值对聚类结果有很大影响。

DBSCAN的主要缺点有：

　　1）如果样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差，这时用DBSCAN聚类一般不适合。

　　2） 如果样本集较大时，聚类收敛时间较长，此时可以对搜索最近邻时建立的KD树或者球树进行规模限制来改进。

　　3） 调参相对于传统的K-Means之类的聚类算法稍复杂，主要需要对距离阈值ϵ，邻域样本数阈值$m(MinPts)$联合调参，不同的参数组合对最后的聚类效果有较大影响。

OPTICS:通过点排序识别聚类结构

在前面介绍的DBSCAN算法中，有两个初始参数Eps（邻域半径）和minPts(Eps邻域最小点数)需要手动设置，并且聚类的结果对这两个参数的取值非常敏感，不同的取值将产生不同的聚类结果。为了克服DBSCAN算法这一缺点，提出了OPTICS算法（Ordering Points to identify the clustering structure），翻译过来就是，对点排序以此来确定簇结构。

OPTICS是对DBSCAN的一个扩展算法。该算法可以让算法对半径Eps不再敏感。只要确定minPts的值，半径Eps的轻微变化，并不会影响聚类结果 。OPTICS并不显示的产生结果类簇，而是为聚类分析生成一个增广的簇排序，从这个排序中可以得到基于任何参数Eps和minPts的DBSCAN算法的聚类结果。

核心距离与可达距离

要搞清楚OPTICS算法，需要搞清楚2个新的定义：核心距离和可达距离。

• 核心距离：一个对象p的核心距离是使得其成为核心对象的最小半径，如果p不是核心点，其可达距离没有定义 。
• 可达距离：从q到p的可达距离是$\max \{core-distance(q), dist(p,q)\}$。如果q不是核心点，其从q到p的可达距离没有定义。另外对象p关于不同的核心对象，p可能有多个可达距离。p的最小可达距离代表离一个稠密簇的距离越短，越处于核心密集地段。

举例，下图中假设minPts=3，半径是ϵϵ。那么P点的核心距离是d(1,P)，点2的可达距离是d(1,P)，点3的可达距离也是d(1,P)，点4的可达距离则是d(4,P)的距离。

OPTICS算法描述

输入：样本集D, 邻域半径ϵϵ, 给定点在ϵϵ领域内成为核心对象的最小领域点数MinPts

输出：具有可达距离信息的样本点输出排序

首先创建两个队列，有序队列和结果队列。（有序队列用来存储核心对象及其该核心对象的直接可达对象，并按可达距离升序排列；结果队列用来存储样本点的输出次序。你可以把有序队列里面放的理解为待处理的数据，而结果队列里放的是已经处理完的数据）。

步骤：

• D: 待聚类的集合
• Q: 有序队列，元素按照可达距离排序，可达距离最小的在队首
• O: 结果队列，最后输出结果的点集的有序队列

首先从D中取出一个核心对象p，首先p要先标记加入结果队列，它的领域则加入有序队列。从有序队列取队首q，先把队首q标记且加入结果队列，若q不为核心对象则继续从Q队列中取队首处理；否则若为核心队列则将q的领域加入到有序队列并重新排列顺序。加入新元素后再取有序队列队首依次循环处理。算法结束，输出结果队列中的有序样本点。

得到结果队列后，使用如下算法得到最终的聚类结果：

• 从结果队列中按顺序取出点，如果该点的可达距离不大于给定半径ϵϵ，则该点属于当前类别，否则至步骤2
• 如果该点的核心距离大于给定半径ϵ，则该点为噪声，可以忽略，否则该点属于新的聚类，跳至步骤1
• 结果队列遍历结束，则算法结束

上面的算法处理完后，我们得到了输出结果序列，每个节点的可达距离和核心距离。我们以可达距离为纵轴，样本点输出次序为横轴进行可视化：

其中：

• X轴代表OPTICS算法处理点的顺序，Y轴代表可达距离。
• 簇在坐标轴中表述为山谷，并且山谷越深，簇越紧密
• 黄色代表的是噪声，它们不形成任何凹陷。

当你需要提取聚集的时候，参考Y轴和图像，自己设定一个阀值就可以提取聚集了。再来一张凹陷明显的：

OPTICS的核心思想：

• 较稠密簇中的对象在簇排序中相互靠近
• 一个对象的最小可达距离给出了一个对象连接到一个稠密簇的最短路径

DPCA算法

2014年6月，Alex Rodriguez和Alessandro Laio在ScienceScience上发表了一篇名为《Clustering by fast search and find of density peaks》的文章，提供了一种简洁而优美的聚类算法，是一种基于密度的聚类方法，可以识别各种形状的类簇，并且参数很容易确定。它克服了DBSCAN中不同类的密度差别大、邻域范围难以设定的问题，鲁棒性强。 在文章中提出的聚类方法DPCA算法（Desity Peaks Clustering Algorithm）基于这样一种假设：对于一个数据集，聚类中心被一些低局部密度的数据点包围，而且这些低局部密度点距离其他有高局部密度的点的距离都比较大。

一些概念：

• 局部密度$p_i$ ：即到对象i的距离小于$d_c$的对象个数。
• 高局部密度点距离（顾名思义，密度是特别局部的），其定义为：

即在局部密度高于对象i的所有对象中，到对象i最近的距离。 而极端地，对于局部密度最大的那个对象(它没有比它更大的了)，我们设置$\delta=max(d_{ij})$，即它与离它最远的点的距离； 只有那些密度是局部或者全局最大的点（即稀疏的点）才会有远大于正常值的高局部密度点距离。

聚类过程

这个聚类实例摘自作者的PPT讲演，在一个二维空间中对数据进行聚类，具体步骤如下：

1、首先计算每一个点的局部密度ρiρi，如图中，$ρ_1=7,ρ_8=5,ρ_{10}=4$

2、然后对于每一个点i计算在局部密度高于对象i的所有对象中，到对象i最近的距离，即$ \delta_i $

3、对每一个点，绘制出局部密度与高局部密度点距离的关系散点图

4、图上的异常点即为簇中心。如图所示，1和10两点的局部密度和高局部密度距离都很大，将其作为簇中心。

5、将其他的点分配给距离其最近的有着更高的局部密度的簇。

左图是所有点在二维空间的分布，右图是以ρρ为横坐标，以δδ为纵坐标绘制的决策图。容易发现，1和10两个点的$ρ_i$和$ \delta_i $都比较大，作为簇的中心点。26、27、28三个点的δδ也比较大，但是ρ比较小，所以是异常点。

簇中心的识别

那些有着比较大的局部密度ρiρi和很大的高局部密度δiδi的点被认为是簇的中心； 而高局部密度距离δiδi较大但局部密度ρiρi较小的点是异常点； 确定簇中心之后，其他点按照距离已知簇的中心最近进行分类，也可以按照密度可达的方法进行分类。

但是，这里我们在确定聚类中心时，没有定量地分析，而是通过肉眼观察，包含很多的主观因素。因此，作者在文中给出了一种确定聚类中心个数的提醒：计算一个将ρ值和$ \delta$值综合考虑的量

显然γ值越大，越有可能是聚类中心。因此，只需对其降序排列，然后从前往后截取若干个数据点作为聚类中心就可以了。

领域阈值$d_c$的选择：一种推荐做法是选择$d_c$，使得平均每个点的邻居数为所有点的1%~2%。

基于网格的聚类

基于格子的参考这篇文章吧，感觉很少用啊，主要是STING统计信息网格算法和CLIQUE子空间聚类算法。

戳我

谱聚类

谱聚类似乎也应用较广，这篇博客写的很清晰了

戳我

下图简单地总结了一些聚类方法的简单划分

基于划分的聚类

聚类分析最简单、最基本的版本是基于划分的聚类，它把对象组织成多个互斥的组或簇。为了使得问题说明简洁，我们假定簇个数作为背景知识给定，这个参数是划分方法的起点。

k-均值（k-mean） ：一种基于形心的技术

k均值算法非常简单，它用簇$C_i$的形心代表该簇。每次确定K个类别中心，然后将各个结点归属到与之距离最近的中心点所在的Cluster，然后将类别中心更新为属于各Cluster的所有样本的均值，反复迭代，直至类别中心不再发生变化或变化小于某阈值。 下面给出该算法的伪代码

• 优点：
  • 是解决聚类问题的一种经典算法，简单、快速
  • 对处理大数据集，该算法保持可伸缩性和高效率
• 缺点：
  • 必须事先给出K，而且对初值敏感，对于不同的初始值，结果可能不同
  • 只能发现球状Cluster，不适合于发现非凸形状的簇或者大小差别很大的簇
  • 对噪声和孤立点数据敏感，如簇中含有异常点，将导致均值偏离严重

如何确定k类

https://www.cnblogs.com/yan2015/p/5239970.html

k-中心点（k-mediods）：一种基于代表对象的技术

k-均值算法对离群点敏感，因为这种对象远离大多数数据，因此分配到一个簇时，它们可能严重地扭曲簇的均值。因此，提出了k-中心点算法，它挑选实际对象代表簇，每个簇使用一个代表对象。这个代表对象选择的规则是：选择簇内一个点到其他点的距离之和的最小代价值，作为新的中心点。

K-中心聚类算法计算的是某点到其它所有点的距离之和最小的点，通过距离之和最短的计算方式可以减少某些孤立数据对聚类过程的影响 。下面给出算法的伪代码

基于层次的聚类

尽管基于划分的聚类算法能够实现把数据集划分成指定数量的簇，但是在某些情况下，需要把数据集划分成不同层上的簇。层次聚类方法将数据组成层次结构或簇的”树”

基于层次的聚类算法（Hierarchical Clustering）可以是凝聚的（Agglomerative）或者分裂的（Divisive），取决于层次的划分是“自底向上”还是“自顶向下”。

• 自顶向下： 它把所有对象至于一个簇中开始，该簇是层次结构的根。然后，它把根上的簇划分为多个较小的子簇，并且递归地把这次簇划分成更小的簇，直到满足终止条件。常见的自顶向下的算法有K-means层次聚类算法。
• 自底向上：把数据集中的每个对象最为一个簇开始，迭代地把簇合并成为更大的簇，直到最终形成一个大簇，或者满足某个终止条件。基于自底向上算法有凝聚算法、BIRCH算法、CURE算法、变色龙算法等。

自顶向下算法

Hierarchical K-means算法

Hierarchical K-means算法是“自顶向下”的层次聚类算法，用到了基于划分的聚类算法那K-means，算法思路如下：

1. 首先，把原始数据集放到一个簇C，这个簇形成了层次结构的最顶层；
2. 使用K-means算法把簇C划分成指定的K个子簇$C_i，i=1,2,…,k$，形成一个新的层；
3. 对于步骤2所生成的K个簇，递归使用K-means算法划分成更小的子簇，直到每个簇不能再划分（只包含一个数据对象）或者满足设定的终止条件。

如下图，展示了一组数据进行了二次K-means算法的过程

Hierarchical K-means算法一个很大的问题是，一旦两个点在最开始被划分到了不同的簇，即使这两个点距离很近，在后面的过程中也不会被聚类到一起。

对于以上的例子，红色椭圆框中的对象聚类成一个簇可能是更优的聚类结果，但是由于橙色对象和绿色对象在第一次K-means就被划分到不同的簇，之后也不再可能被聚类到同一个簇。

自底向上算法

Agglomerative Clustering算法

相比于Hierarchical K-means算法存在的问题，Agglomerative Clustering算法能够保证距离近的对象能够被聚类到一个簇中，该算法采用的“自底向上”聚类的思路。

算法思路，对于数据集$D，D=x_1,x_2,…,x_n$：

1. 将数据集中的每个对象生成一个簇，得到簇列表$C，C=c_1,c_2,…,c_n$
   • a) 每个簇只包含一个数据对象：$c_i=x_i$；
2. 重复如下步骤，直到C中只有一个簇：
   • a) 从C中的簇中找到两个“距离”最近的两个簇：$\min D(ci,cj)$；
   • b) 合并簇$c_i$和$c_j$，形成新的簇$c_{ij}；
   • c) 从C中删除簇$c_i%和$c_j$，添加簇$c_{ij}

簇间距离计算

在上面描述的算法中涉及到计算两个簇之间的距离，对于簇$C_1$和$C_2$，计算$minD(C1,C2)$，有以下几种计算方式：

最小距离：

两个簇之间最近的两个点的距离作为簇之间的距离，该方式的缺陷是受噪点影响大，容易产生长条状的簇。

最大距离：

两个簇之间最远的两个点的距离作为簇之间的距离，采用该距离计算方式得到的聚类比较紧凑。

均值距离： $m_i$和$m_j$为簇内所有点的均值坐标

平均距离：

一个例子

Agglomerative聚类算法的优点是能够根据需要在不同的尺度上展示对应的聚类结果，缺点同Hierarchical K-means算法一样，一旦两个距离相近的点被划分到不同的簇，之后也不再可能被聚类到同一个簇，即无法撤销先前步骤的工作。另外，Agglomerative性能较低，并且因为聚类层次信息需要存储在内存中，内存消耗大，不适用于大量级的数据聚类，下面介绍一种针对大数据量级的聚类算法BIRCH。

BIRCH算法：使用聚类特征树

BIRCH算法利用了一个树结构来帮助实现快速的聚类，这个数结构类似于平衡B+树，一般将它称之为聚类特征树(Clustering Feature Tree，简称CF Tree)。这颗树的每一个节点是由若干个聚类特征(Clustering Feature，简称CF)组成。从下图可以看看聚类特征树是什么样子的：每个节点包括叶子节点都有若干个CF，而内部节点的CF有指向孩子节点的指针，所有的叶子节点用一个双向链表链接起来。

在聚类特征树中，一个聚类特征CF是这样定义的：每一个CF是一个三元组，可以用（N，LS，SS）表示，其中N代表了这个CF中拥有的样本点的数量；LS代表了这个CF中拥有的样本点各特征维度的和向量，SS代表了这个CF中拥有的样本点各特征维度的平方和。 聚类特征本质上是定簇的统计汇总。使用聚类特征，我们可以很容易地推导出簇的许多有用的统计量，例如簇的形心$x_0$、半径R和直径D分别是

其中，R是成员对象到形心的平均距离，D是簇中逐对对象的平均距离。R和D都反映了形心周围簇的紧凑程度。

此外，聚类特征是可加的，也就是说，对于两个不相交的簇$C_1$和$C_2$，其聚类特征分别是$CF_1[n_1,LS_1,SS_1]$和$CF_2 [n_2,LS_2,SS_2]，合并后的簇的聚类特征是

对于CF Tree，一般有几个重要参数，第一个参数是每个内部节点的最大CF数B，第二个参数是每个叶子节点的最大CF数L，第三个参数是针对叶子节点中某个CF中的样本点来说的，它是叶节点每个CF的最大样本半径阈值T，也就是说，在这个CF中的所有样本点一定要在半径小于T的一个超球体内。对于图中的CF Tree，限定了B=7， L=5， 也就是说内部节点最多有7个CF，而叶子节点最多有5个CF。

将所有的训练集样本建立了CF Tree，一个基本的BIRCH算法就完成了，对应的输出就是若干个CF节点，每个节点里的样本点就是一个聚类的簇。也就是说BIRCH算法的主要过程，就是建立CF Tree的过程。

聚类特征树CF Tree的生成

下面看看怎么生成CF Tree。先定义好CF Tree的参数： 即内部节点的最大CF数B， 叶子节点的最大CF数L， 叶节点每个CF的最大样本半径阈值T。

开始时CF Tree是空的，没有任何样本，我们从训练集读入第一个样本点，将它放入一个新的CF三元组A，这个三元组的N=1，将这个新的CF放入根节点，此时的CF Tree如下图：

现在继续读入第二个样本点，发现这个样本点和第一个样本点A在半径为T的超球体范围内，即他们属于一个CF，将第二个点也加入CF A,此时需要更新A的三元组的值。此时A的三元组中N=2。此时的CF Tree如下图：

此时读取第三个节点，结果发现这个节点不能融入刚才前面的节点形成的超球体内，也就是说，需要一个新的CF三元组B来容纳这个新的值。此时根节点有两个CF三元组A和B，此时的CF Tree如下图：

当来到第四个样本点时，发现和B在半径小于T的超球体，这样更新后的CF Tree如下图：

那个什么时候CF Tree的节点需要分裂呢？假设现在的CF Tree 如下图， 叶子节点LN1有三个CF， LN2和LN3各有两个CF。叶子节点的最大CF数L=3。此时一个新的样本点来了，发现它离LN1节点最近，因此开始判断它是否在sc1,sc2,sc3这3个CF对应的超球体之内，但是很不幸，它不在，因此它需要建立一个新的CF，即sc8来容纳它。问题是我们的L=3，也就是说LN1的CF个数已经达到最大值了，不能再创建新的CF了，怎么办？此时就要将LN1叶子节点一分为二了。

将LN1里所有CF元组中，找到两个最远的CF做这两个新叶子节点的种子CF，然后将LN1节点里所有CF sc1, sc2, sc3，以及新样本点的新元组sc8划分到两个新的叶子节点上。将LN1节点划分后的CF Tree如下图：

如果内部节点的最大CF数B=3，则此时叶子节点一分为二会导致根节点的最大CF数超了，也就是说，根节点现在也要分裂，分裂的方法和叶子节点分裂一样，分裂后的CF Tree如下图：

有了上面这一系列的图，相信大家对于CF Tree的插入就没有什么问题了，总结下CF Tree的插入：

• 1、从根节点向下寻找和新样本距离最近的叶子节点和叶子节点里最近的CF节点（判断新节点与NLN1和NLN2谁近一些，然后继续往下）
• 2、如果新样本加入后，这个CF节点对应的超球体半径仍然满足小于阈值T，则更新路径上所有的CF三元组，插入结束。否则转入3.
• 3、如果当前叶子节点的CF节点个数小于阈值L，则创建一个新的CF节点，放入新样本，将新的CF节点放入这个叶子节点，更新路径上所有的CF三元组，插入结束。否则转入4。
• 4、将当前叶子节点划分为两个新叶子节点，选择旧叶子节点中所有CF元组里超球体距离最远的两个CF元组，分布作为两个新叶子节点的第一个CF节点。将其他元组和新样本元组按照距离远近原则放入对应的叶子节点。依次向上检查父节点是否也要分裂，如果需要按和叶子节点分裂方式相同。

当然，真实的BIRCH算法除了建立CF Tree来聚类，其实还有一些可选的算法步骤的，现在我们就来看看 BIRCH算法的流程。

• 1） 将所有的样本依次读入，在内存中建立一颗CF Tree, 建立的方法参考上一节。
• 2）（可选）将第一步建立的CF Tree进行筛选，去除一些异常CF节点，这些节点一般里面的样本点很少。对于一些超球体距离非常近的元组进行合并
• 3）（可选）利用其它的一些聚类算法比如K-Means对所有的CF元组进行聚类，得到一颗比较好的CF Tree.这一步的主要目的是消除由于样本读入顺序导致的不合理的树结构，以及一些由于节点CF个数限制导致的树结构分裂。
• 4）（可选）利用第三步生成的CF Tree的所有CF节点的质心，作为初始质心点，对所有的样本点按距离远近进行聚类。这样进一步减少了由于CF Tree的一些限制导致的聚类不合理的情况。

从上面可以看出，BIRCH算法的关键就是步骤1，也就是CF Tree的生成，其他步骤都是为了优化最后的聚类结果。

优点

• 1) 节约内存，所有的样本都在磁盘上，CF Tree仅仅存了CF节点和对应的指针。
• 2) 聚类速度快，只需要一遍扫描训练集就可以建立CF Tree，CF Tree的增删改都很快。
• 3) 可以识别噪音点，还可以对数据集进行初步分类的预处理

缺点

• 1) 由于CF Tree对每个节点的CF个数有限制，导致聚类的结果可能和真实的类别分布不同.
• 2) 对高维特征的数据聚类效果不好。此时可以选择Mini Batch K-Means
• 3) 如果数据集的分布簇不是类似于超球体，或者说不是凸的，则聚类效果不好。

CURE算法

CURE（Clustering Using Representatives）是一种针对大型数据库的高效的聚类算法。基于划分的传统的聚类算法得到的是球状的，相等大小的聚类，对异常数据比较脆弱。CURE采用了用多个点代表一个簇的方法，可以较好的处理以上问题。并且在处理大数据量的时候采用了随机取样，分区的方法，来提高其效率，使得其可以高效的处理大量数据。

我们先看一下基于划分聚类算法的缺陷：

如上图所示，基于划分的聚类算法比如Hierarchical K-means聚类算法，不能够很好地区分尺寸差距大的簇，原因是K-means算法基于“质心”加一定“半径”对数据进行划分，导致最后聚类的簇近似“圆形”。

CURE算法核心的思想是使用一定数量的“分散的”点（scattered points）来代表一个簇（cluster），而不像是其他层次聚类算法中，只使用一个点，使得CURE算法有如下优势：

• 准确地识别任意形状的簇；
• 准确地识别尺寸差距大的簇；
• 很好地处理“噪点”

所以，CURE算法很好地解决了上面提到的聚类结果的缺陷，CURE算法主流程如下：

Pass 1

• 1、从总数据中随机选取一个样本；
• 2、利用层次聚类算法把这个样本聚类，形成最初的簇$C_i,(i=1,2,…,k)$；
• 3、选取“代表点”（representative pionts）;

①对于每个簇，选取代表点（比如4个），这些点尽量分散;

②按照固定的比例α（比如20%），把每个样本点向簇的“质心”收缩，生成代表点

Pass 2

• 重新扫描所有的数据， 对于点p，找到距离p最近的簇，把它放到 “最近的簇”。简单来讲，是点p到簇$C_i$的距离为点p到簇$C_i$的四个“代表点 中最近的点之间的距离。

收缩系数α的取值不同，聚类结果也相应不同。当α趋于0时，所有的“代表点”都汇聚到质心，算法退化为基于“质心”的聚类；当α趋于1时，“代表点”完全没有收缩，算法退化为基于“全连接”的聚类，因此α值需要要根据数据特征灵活选取，才能得到更好的聚类结果

Chameleon变色龙算法：使用动态建模

Chameleon（变色龙）是一种层次聚类算法，它采用动态建模来确定一对簇之间的相似度。在Chameleon中，簇的相似性依据以下两点评估：1）簇中对象的连接情况 ；2）簇的邻近性。也就是说，如果两个簇的互连性都很高并且它们之间又靠得很近就将其合并。

整体算法流程：

1、创建KNN图，每个节点将其最相似的k个节点用一条边连接起来；

2、使用最大流算法或者最小割算法，将kNN图分隔成小图； 也就是说簇C被划分为子簇CiCi和$C_j$，使得把C二分成$C_i$和$C_j$而被切断的边的权重之和最小。

3、将小簇进行和并，找对最大的度量值$RC*RI^\alpha$的两个簇，合并条件是$RC*RI^\alpha$大于某个阈值，否则结束合并。RC和RI的一个基本思想是，点之间的链接越多，这些点越可能连接成一个簇，C表示一个簇，是点的集合，|C|是集合的大小，即点的个数, $EC(A,B)$表示两个簇之间的边的数量。

相似互连度$RI(C_i,C_j)$

相对接近度$RC(C_i,C_j)$

其中，分子是连接$C_i$顶点和$C_j$顶点的边的平均权重，分母SECC是最小二分簇$C_i$（或$C_j$）的边的平均权重。

贝叶斯信念网络

基本概念

朴素贝叶斯分类有一个限制条件，就是特征属性必须有条件独立或基本独立（实际上在现实应用中几乎不可能做到完全独立）。当这个条件成立时，朴素贝叶斯分类法的准确率是最高的，但不幸的是，现实中各个特征属性间往往并不条件独立，而是具有较强的相关性，这样就限制了朴素贝叶斯分类的能力。 解决这个问题的一种算法叫贝叶斯网络（又称贝叶斯信念网络或信念网络）。

贝叶斯网络由两个成分定义：1）有向无环图（DAG）; 2)条件概率表的集合(Conditional Probability Table，CPT)

上图给出了一个布尔变量的简单贝叶斯信念网络，图中的弧可看做因果知识。换言之，一旦我们知道变量LungCanner的结果，那么变量FamilyHistory和Smoker就不再提供关于PostiveXRay的任何附近信息。

DAG中每一个节点表示一个随机变量，可以是可直接观测变量或隐藏变量，而有向边表示随机变量间的条件依赖；条件概率表中的每一个元素对应DAG中唯一的节点，存储此节点对于其所有直接前驱节点的联合条件概率。贝叶斯网络有一条极为重要的性质，就是我们断言每一个节点在其直接前驱节点的值制定后，这个节点条件独立于其所有非直接前驱前辈节点。这条特性的重要意义在于明确了贝叶斯网络可以方便计算联合概率分布。 一般情况先，多变量非独立联合条件概率分布有如下求取公式：

而在贝叶斯网络中，由于存在前述性质，任意随机变量组合的联合条件概率分布被化简成

其中，$P(x_1,…,x_n)$是X的值的特定组合的概率，Parents表示xi的直接前驱节点的联合 ，而$P(x_i|Parents(x_i))$的值对应于CPT概率表的值。

上图是一个有向无环图（DAG） ，不过仅有这个图的话，只能定性给出随机变量间的关系，如果要定量，还需要一些数据，这些数据就是每个节点对其直接前驱节点的条件概率（也就是CPT表的概率），而没有前驱节点的节点则使用先验概率表示。

没有前驱的节点用先验概率表示；以及CPT条件概率，例如P(H=0|R=0)=0.9（真实账号为假，头像也为假的概率）

有了这些数据，不但能顺向推断，还能通过贝叶斯定理进行逆向推断。例如，现随机抽取一个账户，已知其头像为假，求其账号也为假的概率：

如果给出所有节点的条件概率表，则可以在观察值不完备的情况下对任意随机变量进行统计推断。上述方法就是使用了贝叶斯网络。

训练贝叶斯网络

构造与训练贝叶斯网络分为以下两步：

• 1、确定随机变量间的拓扑关系，形成DAG。这一步通常需要领域专家完成，而想要建立一个好的拓扑结构，通常需要不断迭代和改进才可以。
• 2、训练贝叶斯网络。如果不训练的，我们只能知道定性的网络，而不能定量。实际上这一步也就是要完成条件概率表(CPT表)的构造，如果每个随机变量的值都是可以直接观察的，像我们上面的例子，那么这一步的训练是直观的，方法类似于朴素贝叶斯分类。但是通常贝叶斯网络的中存在隐藏变量节点，那么训练方法就是比较复杂，例如使用梯度下降法。

性能如何

贝叶斯网络已经广泛于临床，生物，征信等领域。其强大之处在于两点

• 1.贝叶斯网络最强大之处在于从每个阶段结果所获得的概率都是数学与科学的反映，换句话说，假设我们了解了足够多的信息，根据这些信息获继而得统计知识，网络就会告诉我们合理的推断。
• 2.贝叶斯网络最很容易扩展(或减少,简化),以适应不断变化的需求和变化的知识。

使用频繁模式分类

关联分类

回顾一下之前的关联规则，显示了规则的置信度和支持度

从分类角度，置信度类似于规则的准准确度。例如，93%的置信度意味着D中身为年轻人并且信誉度为OK的顾客中，93%属于类buysconputer=yes。支持度20%意味着D中20%的顾客是青年，信誉为OK，并且属于类buyscomputer=yes

一般而言，关联规则的分类包括以下步骤：

• 1、挖掘数据，找出频繁项集，即找出数据经常出现的属性-值对
• 2、分析频繁项集，产生每个类的关联规则，它们满足置信度和支持度标准
• 3、组织规则，形成基于规则的分类器

这里，我们考察以下三种分类方法1）CBA ; 2) CMAR ; 3)CPAR

CBA

最早、最简单的关联分类算法是CBA。CBA使用迭代的方法挖掘频繁项集，类似于Apriori算法。CBA使用了一种启发式方法构造分类器，其中规则按照它们的置信度和支持度递减优先级排序，如果当中一组规则具有相同的前件，则选取具有最高置信度的规则代表该集合。在对新元组分类是，使用满足该元组第一个规则对它进行分类。分类器还包含一个默认规则，具有最低优先级。

CMAR

CMAR和CBA在频繁项集挖掘和构建分类器都不同，CMAR采用FP-growth算法的变形来发现满足最小支持的最小置信度的规则完全集。构造分类器时，如果新元组X只匹配一个规则，则简单地把规则的类标号给这个元组。如果多个规则满足X，把这些规则形成一个集合S。CBA将集合S中最大置信度的规则的类标号指派给X，而CMAR考虑多个规则。它根据S的类标号将规则分类，不同组中的规则具有不同的类标号，然后CMAR使用X2X2卡方度量，根据组中规则的统计相关联找出相关性“最强的”规则组，再把该类标号指派个X元组。这样，它就考虑了多个规则，不是像CBA一样只考虑一个规则。CMAR在准确率和复杂的都比CBA更有效一点。

CPAR

CPAR和CMAR相差不多，它通过FOIL算法而不是FP-growth来挖掘规则。同样也将集合S的规则按类分组。然而，CPAR根据期望准确率，使用每组中最好的k个规则预测X元组的类标号，通过考虑组中最好的k个规则而不是所有规则。在大数据集上，CPAR和CMAR准确率差不多，但产生的规则要比CMAR少的多。

基于有区别力的频繁模式分类

如果我们把所有频繁模式都添加到特征空间，可能许多模式是冗余，还可能因特征太多而过分拟合，导致准确率降低。因此，一种好的做法是使用特征选择，删除区别能力较弱的特征，其一般框架步骤(两步法)如下：

• 特征产生：频繁模式的集合F形成候选特征
• 特征选择： 通过信息增等度量对F进行特征选择，得到选择后的频繁模式FsFs，数据集DD变换成D′D′
• 学习分类模型：在数据集D′D′建立分类器

为了提高两步法的效率，考虑将步骤1和步骤2合并为一步。即有可能只挖掘具有高度区别能力的频繁模式的集合，而不是完全集。DDPMine算法采用这种方法，它首先把训练数据变换到一个称频繁模式树或FP树的紧凑树结构，然后再该树种搜索有区别能力的模式。

在准确率和效率两个方面，DDPMine都优于最先进的关联分类方法。

k-近邻分类

对于，k-近邻分类算法，位置元组每次都被指派到它的k个最近邻（距离度量）的多数类。

这一章很多概念都是之前就接触了，就不一一记录了，这里记录一些感兴趣的吧。

决策树剪枝

为了避免决策树过拟合数据，一般要对决策树进行剪枝：先剪枝和后剪枝

在先剪枝方法中，通过提前停止树的构造（例如，通过决定在给定的结点上不再分裂或划分训练样本的子集）而对树“剪枝”。在构造树时，统计意义下的度量，如信息增益、基尼指数等，可以用于评估分裂的优劣。如果在一个结点划分样本将导致低于预定义阈值的分裂，则给定子集的进一步划分将停止。然而，选取一个适当的阈值是困难的。较高的阈值可能导致过分简化的树，而较低的阈值可能使得树的化简太少。

第二种更常用的方法是后剪枝，它由“完全生长”的树之后再剪去分枝，通过用叶子节点替换要删除的分枝。CART使用的代价复杂度剪枝算法是后剪枝方法的一个实例。该方法把树的复杂度看做树叶节点的个数和树的错误率的函数，如果减去节点N的子树导致较小的代价复杂度，则剪掉该子树；否则，保留该子树。

可伸缩性与决策树

已有的决策树算法，如ID3、C4.5和CART都是为相对较小的数据集规模。另外，大部分情况下，大规模的训练数据不能放在内存！因此，由于训练元组在主存和高速缓存换进换出，决策树的构造可能变得效率低下。最近，已经提出了一些可以解决伸缩问题的决策树算法，例如，RainForest（雨林）能适应可用的内存量，采用了一种新的数据结构形式。

转为AVC集的聚集信息的数据结构来存放

另外一种方法是采用树构造的自助乐观算法（BOAT），它采用了统计学计数，创建给定训练数据的一些较小的样本（或子集），其中每个子集都能放在内存中。使用每个子集构造一颗树，导致多棵树，并使用它们构造一个新树。

使用IF-THEN规则分类

基于规则的分类器使用一组IF-THEN规则进行分类。一个IF-THEN的规则R1一般表示形式有如下两种

1
2
3

R1:IF age=youth AND student=yes THEN buys_conmputer = yes 

R1:IF age=youth ^ student=yes THEN buys_computer = yes

规则R可以用覆盖率和准确率来评估。给定类标记的数据集D中的一个元组X，设$n_{covers}$为规则R覆盖的元组数，$n_{covers}$为R正确分类的元组数，|D|是D中的总元组数，可将R的覆盖率和准确率定义为：

如何建立基于规则的分类器呢

• 1、根据决策树提取规则

对从根到树叶节点的每条路经创建一个规则。沿着给定路经上的每个属性-值的逻辑AND形成规则前件（“IF”部分）。叶结点包含类预测，形成规则后件（“THEN”部分）。由于这些规则都是直接从书中提取的，所以它们是互斥的和穷举的（互斥意味不可能存在规则冲突），因此规则的序不重要——它们是无序的。

由于每个树叶对应一个规则，所以提取的规则集的量也很多。所以有两种解决方法，第一种是先对决策树剪枝，然后提取规则。另外一种是直接提取规则，然后修剪规则，对于不能提高规则的估计准确率的任何条件都可以删减，从而泛化该规则。

• 2、使用顺序覆盖算法

顺序覆盖算法是最广泛使用的挖掘分类规则取集的方法，有许多流行的顺序覆盖算法，包括AQ、CN2和最近提出的RIPPER。算法的一般策略如下：一次学习一个规则，每学习一个规则，就删除该规则覆盖的元组，并在剩下的元组上重负该过程。

从最一般的规则开始，即从规则前件条件为空的规则开始。该规则是：

1

IF  THEN loan_decision = accept

然后，我们考虑每个可以添加到该规则中可能属性测试。Learn_One_Rule采用一种贪心策略，每次选择最能提高规则质量的属性。目前，我们使用规则的准确率作为质量度量。假设Learn_One_Rule发现属性测试income=high最大限度地提高了当前（空）规则的准确率。把它添加到条件中，当前规则变成

1

IF income=high THEN loan_decision = accept

下一次迭代时，再次考虑可能的属性测试，结果选中credit_rating=excellent，当前规则增长，变成

1

IF income=high AND credit_rating=excellent THEN loan_decision = accept

重复该过程，直到结果规则达到可接受的质量水平。另外，贪心策略如果不自觉选到一个很差的属性怎么办，为了减少这种发生的几率，可以选出最好的k个而不是最好的一个属性添加到当前规则。

规则质量的度量

Learn_One_Rule需要度量规则的质量，之前我们用的是准确率。但准确率本身并非规则质量的可靠估计。这里介绍几个相对有用的几种度量：1）、熵 ；2）、信息增益；3）考虑覆盖率的统计检验

我们想知道给定属性测试到condition中是否导致更好的规则，我们称新的条件为condition’，换言之，我们想知道R’是否比R好。

熵：D是condition’覆盖元组集合，而$p_i$是D中$C_i$类的概率。熵越小，condition’越好。熵更偏向于覆盖单个类大量元组和少量其他类元组的条件。

信息增益：FOIL算法是一种学习一阶逻辑规则的顺序覆盖算法，FOIL用下式估计扩展condition’s而获得信息

它偏向于具有高准确率并且覆盖许多正元组的规则

似然率统计量

其中，m是类数，$f_i$是这些元组类i的观测概率，$e_i$是规则随机预测时类i的期望频率。似然率有助于识别具有显著覆盖率的规则。

CN2使用熵和似然率检验，而FOIL的信息增益被RIPPER使用。

规则剪枝

之前说了可以在决策树生成之后对规则剪枝，有很多剪枝策略。这里介绍FOIL使用的一种简单但很有效的方法，给定规则R，有：

其中，pos和neg分别为规则R覆盖的正元组数和负元组数。这个值将随着R在剪枝集上的准确率增加而增加。因此，如果R剪枝后版本的FOIL_Prune值较高，则对R剪枝。

如何使用规则分类器来预测元组类标号呢？

如果正常的话，R1是唯一满足的规则，则该规则激活，返回X的类预测。但如果有多个规则被触发，它们指定了不同的类，这时则需要一种解决冲突的策略来决定激活哪一个规则。我们考察两种，即规模序和规则序：

规模序：方案吧最高优先权赋予给”最苛刻”要求的规则，其中苛刻性用规则前件的规模度量（类似于树的深度）

规则序：这种序可以是基于类的或基于规则的。使用基于类的序，类按”重要性”递减排序，如按普遍性的降序排序；基于规则的序，或者根据领域专家的建议，把规则组织成一个优先权列表。

使用统计显著性检验选择模型

在前面我们已经使用了 一些策略来测算分类器的准确率（例如K折交叉验证）。在这里，我们假设经处理，最后生成了两个分类器，他们的评估度量都不相同，那么我们应该选择哪个分类器呢？

直观的看法当然是选择指标好的那个分类器呀，但是 实际上这种差别很有可能是偶然的。我们为了判定这种差别是否是偶然的，还需要进行统计显著性检验。 此外，希望得到平均错误率的置信界，使得我们可以做出这样的陈述：”对于未来样本的95%，观测到的均值将不会偏离正、负两个标准差”或者”一个模型比另外一个模型好，误差幅度为±4±4”

这里用的是显著性检验是t-检验。知乎上给出了相关的解释 ： 知乎t检验解释 https://www.zhihu.com/question/60321751/answer/399954823

对于10-折交叉验证（k=10）的第ii轮，设$err(M_1)_i$(或$err(M_2)_i$)是模型$M_1$(或$M_2$)在第i轮的错误率。对$M_1$的错误率取平均值得到$M_1$的平均错误率，记为$\overline {err}(M_1)$，类似的，可以得到$\overline {err}(M_2)$。两个模型差的方差记为$var(M_1-M_2)$。在我们的例子中，k=10，这里的k个样本是从每个模型的10-折交叉验证得到的错误率。逐对比较t-统计量按下式计算：

其中

为了计算$M_1$和$M_2$是否显著不同，计算t并选择显著水平sig。实践中，通常使用5%或1%的显著水平。然后，查找t-分布表。通常该表以自由度为行（k个样本具有k-1个自由度，对于我们的例子，自由度为9），显著水平为列。假定要确定$M_1$和$M_2$之间的差对总体的95%（即sig=5%或0.05）是否显著不同。然而，由于t分布是对称的，通常只显示分布上部的百分点，因此，找z=sig/2=0.025的表值，其中z也称为置信界。如果t>z或t<-z，则t落在拒斥域，在分布的尾部。这意味着可以拒绝$M_1$和$M_2$的均值相同的原假设，并断言两个模型之间存在统计的显著的差别。否则，如果不能拒绝原假设，于是断言$M_1$和$M_2$之间的差可能是随机的。

如果有两个检验集而不是单个检验集，则使用t-检验的非逐对版本，其中两个模型的均值之间的方差估计为：

其中，k1和k2分别用于M1和M2的交叉验证样本数（在我们的情况下，10-折交叉验证的轮）。这也称为两个样本的t检验。在查t分布表时，自由度取两个模型的最小自由度。

于大量的研究、问题的多方面扩展和广泛的应用研究。频繁模式挖掘已经远远超过了事务数据。这里，我们介绍其他多种挖掘模式类型的方法，包括多层模式、多维模式、稀有模式、负模式、受约束的频繁模式和巨型模式挖掘。书上的内容都是比较浅显，更多的是介绍性的东西，可能需要到实际工作上才能理解更深一些。

挖掘多层关联规则

对于许多应用，在较高的抽象层（抽象的大类，例如电脑，而不是具体某种品牌和型号的电脑）发现的强关联规则，可能有很高的支持度，但可能是常识性知识。我们希望往下钻，在更细节的层次发现新颖的模式。另外一方面，在较低或原始抽象层，可能有太多的零散模式，其中一些只不过是较高层模式的平方特化。

在这种较低层或原始层数据中很难发现有趣的规则模式，例如，“Dell Studio XPS 16 Notebook”和“Logitech VX Nano Cordless Laser Mouse”每个都在很少一部分事务中出现，则可能很难找到涉及它们的强关联规则。少数人同时购买它们，使得该商品集不太可能满足最小支持度。然而，我们预料，在这些商品的泛化抽象之间，如在”Dell Notebook” 和”Cordless Mouse”之间，可望更容易发现强规则。这种在多个抽象层的数据上挖掘产生的规则称为多层关联规则，一般采用如下自顶向下的方法：

• 对于所有层使用一致的支持度（称作一致支持度）：在每一层挖掘时，使用相同的最小支持度阈值

然而，一致支持度方法有一些困难。较低层次抽象的项不大可能象较高层次抽象的项出现得那么频繁。如果最小支持度阈值设置太高，可能丢掉出现在较低抽象层中有意义的关联规则。如果阈值设置太低，可能会产生出现在较高抽象层的无兴趣的关联规则。这导致了下面的方法：

• 在较低层使用递减的支持度（称作递减支持度）：每个抽象层有它自己的最小支持度阈值。抽象层越低，对应的阈值越小。
• 使用基于项或基于分组的最小支持度：例如，用户可以根据产品价格或者根据感兴趣的商品设置最小支持度，对如”价格超过1000美元的照相机”或”平板电脑” 设置特别低的支持度，以便特别关注这类商品的关联模式

为了从具有不同支持度阈值的组中挖掘混合项模式，通常在挖掘中取所有组的最低支持度阈值。这将避免过滤掉有价值的模式，该模式包含来自具有最低支持度阈值组的项。同时，每组的最小支持阈值应该保持，以免从每个组产生无趣的项集。

检查多层关联规则冗余性

挖掘多层关联规则一个严重的副作用是，由于项之间的“祖先”关系，可能产生一些多个抽象层上的冗余的规则，例如：”desktop computer”是”IBM desktop computer”的祖先，有以下规则：

如果后一个具有较小一般性的规则不提供新的信息，应当删除它。让我们看看如何来确定。规则 R1 是规则 R2 的祖先，如果R1能够通过将R2中的项，用它在概念分层（分配比率）中的祖先替换得到，则可以将R2删除。

以上诉规则例子：假定规则(6.9)具有 70%置信度，8%支持度，并且大约四分之一的”desktop computer”销售是”IBM desktop computer”。可以期望规则(6.10)具有大约 70%的置信度（由于所有的”IBM desktop computer”样本也是” desktop computer”样本）和 2%（即，8%×1/4）的支持度。也就是说，根据实际销量的分层可以通过R1推到出R2的规则与规则(6.10)相差无几，则R2规则是冗余的。

挖掘多维关联规则

本节，你将学习挖掘多维关联规则的方法。多维关联规则是涉及多个属性或谓词的规则（例如，关于顾客的 buys 和顾客的 age 的规则）。我们把规则中每个不同的谓词称作维。例如：

其中，数据库属性可能是分类属性和量化属性（数值），对于量化属性，挖掘多维相关规则的计数可以分为两种基本方法：

• 第一种方法：使用预定义的概念分层对量化属性离散化，例如，income 的概念分层可以用于以区间值，如“0…20K”代替
• 第二种方法：根据数据的分布，将量化属性离散化或聚类到“箱”

正如前面讨论的，我们可以把量化属性离散化为多个区间，而后在关联挖掘时把它们看做是分类属性。然而，这种简单的离散化可能导致产生大量的规则，其中许多规则可能没什么用。这里我们介绍三种方法，帮助克服这一困难，以便发现新颖的关联关系：

• 1、数据立方体方法
• 2、基于聚类的方法
• 3、揭示异常行为的统计学方法

挖掘稀有模式和负模式

迄今为止，介绍的都是挖掘频繁模式，然而，有时令人感兴趣的不是频繁模式，而是发现稀有的模式（例如钻石表的销售是稀有的），或发现反映项之间的负相关的模式（例如发现顾客频繁地购买经典可口可乐或无糖可乐，但不可能一起都买）。

• 稀有模式：是指其支持度低于（或远低于）用户指定的最小支持度阈值的模式。然而，由于大多数项集的出现频度通常都低于甚至远低于最小支持度阈值，因此实践中允许用户指定稀有模式的其他条件是可取的。
• 负相关模式：如果项集X和Y 都是频繁的，但很少一起出现$(sup(X \cup Y) < sup(X) \times sup(Y))$ ，则项集X和Y是负相关的，并且$X\cup Y$ 是负相关模式.如果$(sup(X \cup Y) \ll sup(X) \times sup(Y))$， 则项集X和Y是强负相关的，并且$X\cup Y$是强负相关模式。

然而，上面这个公式度量不是零不变的，只能有效地解决非零事务的数据。如果数据库存在大量的零事务，则应该使用零不变度量Kulczynski，下面给出具体定义：

零不变负相关模式：假设项集X和Y都是频繁的，即$sup(X)\geq min_sup$ ，$sup(Y)\geq min_sup$ ， 其中$min_sup$是最小支持度阈值。如果有$(P(X|Y)+P(Y|X))/2<\epsilon$，其中$\epsilon$是负模式阈值，则$X\cup Y$是负相关模式。

基于约束的频繁模式挖掘

作为限制搜索空间的约束条件，这种策略称为基于约束的挖掘。

元规则就是挖掘用户感兴趣的规则的语法形式，例如：

其中，P1和P2是谓词变量，在挖掘过程中被例示为给定数据库的属性；X是变量，代表顾客；Y和W是分别赋给P1和P2的属性值。

对于规则约束，如何使用规则约束对搜索空间进行剪枝？主要有两种方法：1、对模式空间剪枝；2、数据空间剪枝

对模式空间剪枝

根据约束如何与模式挖掘过程配合，模式剪枝约束可以分为五类：1）反单调的；2）单调的；3）简洁的；4）可转变的；5）不可转变的（这个不重要）

• 反单调的：规则约束$”sum(I.price)\leq 100”$，如果一个候选项集中的商品价格和大于 100 美元，则该项集可以由搜索空间剪去，因为向该项集中进一步添加项将会使它更贵，因此不可能满足限制。换一句话说，如果一个项集不满足该规则限制，它的任何超集也不可能满足该规则限制。如果一个规则具有这一性质，则称它是反单调的。
• 单调的：规则约束$”sum(I.price)\geq 100”$，集合中的单价和大于 100，进一步添加更多的项到此项集将增加价格，并且总是满足该限制。因此，在项集 I 上进一步检查该限制是多余的。换言之，如果一个项集满足这个规则限制，它的所有超集也满足。如果一个规则具有这一性质，则称它是单调的。
• 简洁：对于这类约束，我们可以枚举并且仅仅列出所有确保满足该限制的集合。因为有一个精确“公式”，产生满足简洁限制的所有集合，在挖掘过程中不必迭代地检验规则限制
• 可转变的约束：有些限制不属于以上三类。然而，如果项集中的项以特定的次序排列，则对于频繁项集挖掘过程，限制可能成为单调的或反单调的。例如，限制“avg(I.price)”既不是反单调的，也不是单调的。然而，如果事务中的项以单价的递增序添加到项集中，则该限制就成了反单调的。类似的，如果是递减顺序添加则是单调的。

对数据空间剪枝

第二种对基于约束的频繁模式挖掘的搜索空间进行剪枝的方法是对数据空间剪枝。这种策略是剪掉对其后挖掘过程中可满足模式的产生没有贡献的数据片段。例如，对于约束是数据简洁的，如果一个挖掘查询要求被挖掘模式必须包含数码相机，则可以在挖掘过程开始减剪掉所有不包含数码相机的事务。对于约束的反单调的，基于当前模式，如果一个数据项不满足数据反单调约束，则可以剪掉它，因为在剩下的挖掘过程中，它不能对当前模式的超模式的产生有任何贡献。

巨型模式

对于数据库有数百或者数千维的数据，用已介绍方法来挖掘高维数据是非常低效的，一种是使用垂直格式数据，之前已经介绍过了。另外一种新的方向是用模型融合，用于巨型模式，即非常长的模式(例如蛋白质的DNA长序列)。这种方法在模式搜索空间中跳跃，得到巨型频繁模式完全集的一个很好的近似解。

对于Apriori和FP-growth算法，会不可避免产生大量中型模式，使得它不可能达到巨型模式。因此提出了模式融合，它融合了少量较短的频繁模式，形成巨型模式候选。

书上提到了核模式的概念，这里没怎么看懂，觉得是核模式代表了一定的鲁棒性。但是书上也直接给出了推论，巨型模式比较短模式有更多的核模式，更鲁棒。也就是说，如果从该模式中去掉少量项，则结果模式会有类似的支集。巨型模式较低层的核模式叫做核后代。所以基于这个特性，模式融合可以融合少量较短的频繁模式。这也是它为什么被称为模式融合的原因 ，因此巨型模式可以通过合并其核模式的真子集产生，例如， abcef可以通过它的两个核模式ab和cef产生。而不需要用单个项增量地扩展，而是与池中多个模式进行凝聚，这样能够迅速地到达巨型模式。

模型融合包括以下两个阶段：

• 1、池初始化

  模式融合假定有一个短频繁模式的初始池。这是一个短长度的频繁模式挖掘集。这个初始值可以用任意已有的有效挖掘算法挖掘。

• 2、迭代的模式融合

  用户首先指定一个参数K的值（K代表挖掘模式的最大个数），然后从当前池中随机地选取K个种子，对于每个种子，我们找出直径为ττ的球内的所有模式。然后，每个”球“中的所有模式融合在一起，形成一个超模式集，这些超模式形成新的池，然后再从这个新的池子中随机地找到K个种子，然后重复上面的工作，一直迭代，直到不能融合为止

因此，该方法可以绕过中型模式，通往巨型模式。

7.5/7.6的内容暂时不是特别重要，用到再补。