R导论学习笔记（八）：概率分布和条件语句

发表于 | 分类于
字数统计: 1k | 阅读时长 ≈ 4

R 的统计表

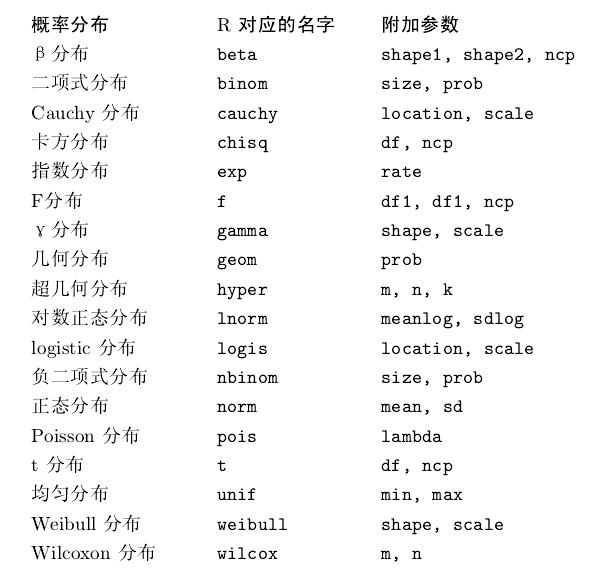
不同的名字前缀表示不同的含义，d表示概率密度函数，p 表示累积分布函数（cumulative distribution function，CDF），q 表示分位函数以及r 表示随机模拟(random deviates)或者随机数发生器

1
2
3
4
5
6
7
8
9
我们可以用很多方法分析一个单变量数据集的分布。最简单的办法就是直接看数字。利用函数summary 和fivenum 会得到两个稍稍有点差异的汇总信息。 此外，stem(“茎叶”图)也会反映整个数据集的数字信息。用函数hist 绘制柱状图。


> hist(eruptions)
> ## 让箱距缩小，绘制密度图
> hist(eruptions, seq(1.6, 5.2, 0.2), prob=TRUE)    # seq为范围和箱距，prob为T时显示频率，F时为频数
> lines(density(eruptions, bw=0.1))
> rug(eruptions) # 显示实际的数据点
更为精致的密度图是用函数density 绘制的。在这个例子中，我们加了一条由density 产生的曲线。你可以用试错法（trial-and-error）选择带宽bw（bandwidth）因为默认的带宽值让密度曲线过于平滑

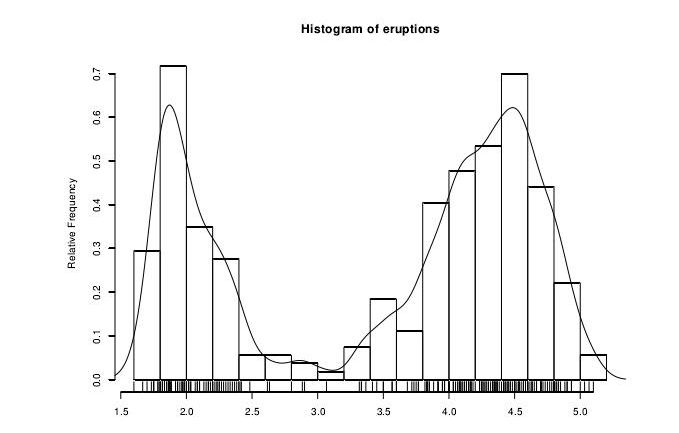
函数ecdf 绘制一个数据集的经验累积分布（empirical cumulativedistribution）函数。

分位比较图（Quantile-quantile (Q-Q) plot），又称QQ图，通常用于检验是否满足正态分布

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#    检验是否符合正态分布
norm.test<- function(input.data,alpha=0.05,pic=TRUE){
    if(pic==TRUE){#画图形
           dev.new()    # 打开一个新的图形窗口
           par(mfrow=c(2,1))    # 一个图版显示2行,3列
           qqnorm(input.data,main="qq图")    
           qqline(input.data)    # 画出QQ图
           hist(input.data,frep=F,main="直方图和密度估计曲线")
           lines(density(input.data),col="blue") #密度估计曲线
           x<- c(round(min(input.data)):round(max(input.data)))
           lines(x,dnorm(x,mean(input.data),sd(input.data)),col="red") #正态分布曲线
    }
    sol<- shapiro.test(input.data)
    if(sol$p.value>alpha){
        print(paste("success:服从正态分布,p.value=",sol$p.value,">",alpha))    
    }else{
         print(paste("error:不服从正态分布,p.value=",sol$p.value,"<=",alpha))
    }
    sol
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
利用Shapiro-Wilk方法进行正态检验
> shapiro.test(long)
Shapiro-Wilk normality test
data: long
W = 0.9793, p-value = 0.01052
检验结果，因为W接近1，p值大于0.05，所以数据为正态分布

利用R自带的Kolmogorov-Smirnov 检验，Kolmogorov-Smirnov检验需要三个输入变量，及数据本身、均值及标准差
> ks.test(long, "pnorm", mean = mean(long), sd = sqrt(var(long)))
One-sample Kolmogorov-Smirnov test
data: long
D = 0.0661, p-value = 0.4284
alternative hypothesis: two.sided
检验结果，因为p值大于0.05，所以数据为正态分布
1
2
3
4
5
6
7
8
9
到现在为止，我们已经学会了单样本的正态性检验。而更常见的操作是比较两个样本的特征。在R 里面，所有“传统”的检验都放在包stats 里面。这个包常常会自动载入。
盒状图（boxplot）为这两组数据提供了简单的图形比较。

A <- scan()
79.98 80.04 80.02 80.04 80.03 80.03 80.04 79.97
80.05 80.03 80.02 80.00 80.02
B <- scan()
80.02 79.94 79.98 79.97 79.97 80.03 79.95 79.97
boxplot(A, B)

箱型图解释

通俗理解T检验和F检验

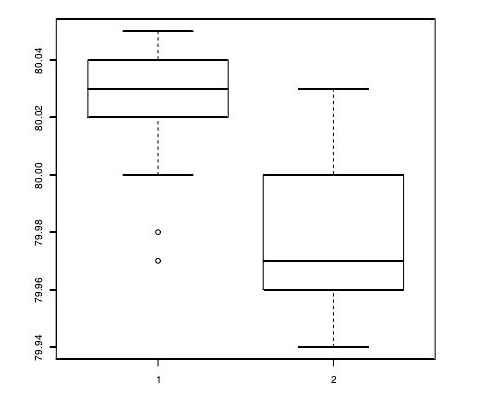
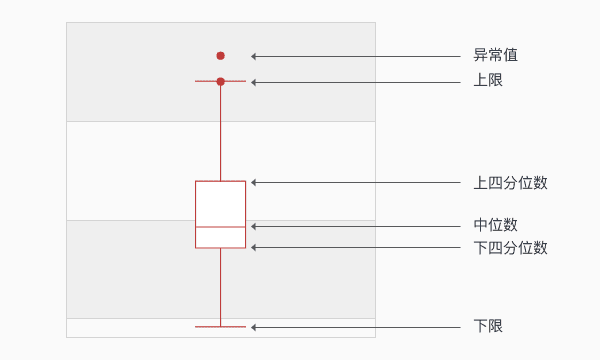
简单来说，通过把所得到的统计检定值与统计学家建立了一些随机变量的概率分布进行比较，证明样本的统计结果不是随机得到的，是有意义的。专业上，P值或sig值为结果可信程度的一个递减指标，如p=0.05提示样本中变量关联有5%的可能是由于偶然性造成的。即假设总体中任意变量间均无关联。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
R 语言的条件语句形式为

> if (expr1) expr2else expr3
R 语言有下面形式的for 循环架构

> for (name in expr 1 ) expr 2
其他循环语句包括

> repeat expr
和语句

> while (condition) expr
关键字break可以用于结束任何循环，甚至是非常规的。它是结束repeat 循环的唯一办法。
关键字next 可以用来结束一次特定的循环，然后直接跳入“下一次”循环
-------------Thanks for Reading!-------------