最大期望算法

发表于 | 分类于
字数统计: 3.6k | 阅读时长 ≈ 15

注：这篇文章原文出处放在了下面的连接，有适当的修改和增加内容，写在这里是为了更好地查阅巩固。

戳我原文

EM算法简介

最大期望算法（Expectation Maximization，简称EM算法）是在概率模型中寻找参数最大似然估计或者最大后验估计的算法，其中概率模型依赖于无法观测的隐藏变量。其主要思想就是通过迭代来建立完整数据的对数似然函数的期望界限，然后最大化不完整数据的对数似然函数。最大期望算法是一种迭代优化算法，其计算方法是每次迭代分为期望(E)步和最大(M)步。

EM算法实例

假如现在我们有两枚硬币1和2，随机抛掷后面朝上概率分别为P1，P2。为了估计两硬币概率，我们做如下实验，每次取一枚硬币，连掷5次后得到如下结果。

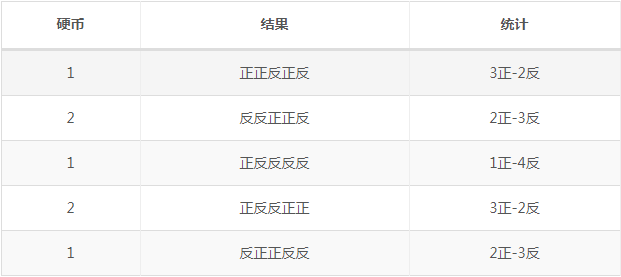
我们可以很方便的估计出硬币1概率P1=0.4，硬币2概率P2=0.5。

下面我们增加问题难度。如果并不知道每次投掷时所使用的硬币标记，那么如何估计P1和P2呢?

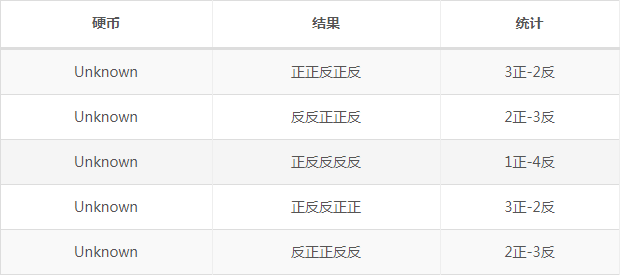
此时我们加入隐含变量z，可以把它认为是一个5维的向量(z1,z2,z3,z4,z5)，代表每次投掷时所使用的硬币。比如z1就代表第一轮投掷时所使用的是硬币1还是2，我们必须先估计出z，然后才能进一步估计P1和P2

我们先随机初始化一个P1和P2，用它来估计z，然后基于z按照最大似然概率方法去估计新的P1和P2.例如假设P1=0.2和P2=0.7，然后我们看看第一轮投掷的最可能是哪个硬币。如果是硬币1，得出3正2反的概率为0.2×0.2×0.2×0.8×0.8=0.00512，如果是硬币2，得出3正2反的概率为0.7×0.7×0.7×0.3×0.3=0.03087。然后依次求出其他4轮中的相应概率，接下来便可根据最大似然方法得到每轮中最有可能的硬币。

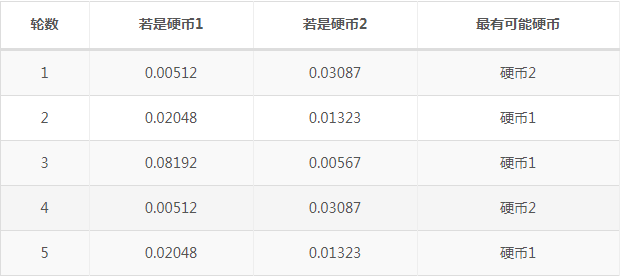
我们把上面的值作为z的估计值(2,1,1,2,1)，然后按照最大似然概率方法来估计新的P1和P2。得到

可以预估，我们继续按照上面思路，用估计出的P1和P2再来估计z，再用z来估计新的P1和P2，反复迭代下去，可以最终得到P1=0.4，P2=0.5。然后无论怎样迭代，P1和P2的值都会保持0.4和0.5不变，于是我们就找到P1和P2的最大似然估计。

上面我们用最大似然方法估计出z值，然后再用z值按照最大似然概率方法估计新的P1和P2。也就是说，我们使用了最有可能的z值，而不是所有的z值。如果考虑所有可能的z值，对每一个z值都估计出新的P1和P2，将每一个z值概率大小作为权重，将所有新的P1和P2分别加权相加，这样估计出的P1和P2是否会更优呢?

但所有的z值共有2^5=32种，我们是否进行32次估计呢？当然不是，我们利用期望来简化运算。

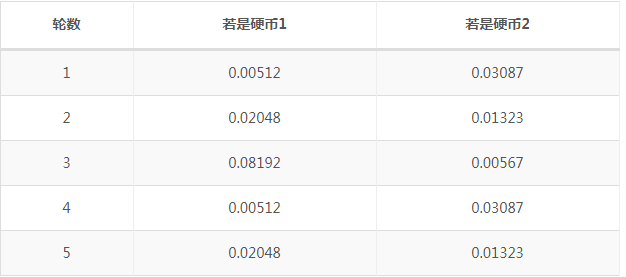
利用上面表格，我们可以算出每轮投掷种使用硬币1或者使用硬币2的概率。比如第一轮使用硬币1的概率

相应的算出其他4轮的概率。

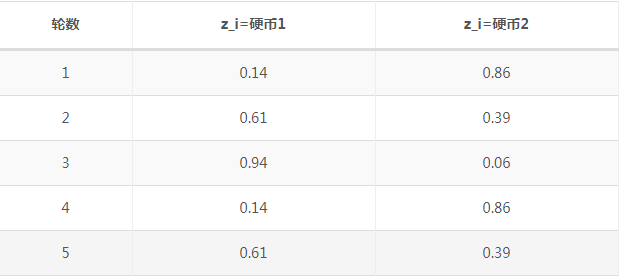
上表中表示期望值，例如0.86表示此轮中使用硬币2的概率是0.86。前面方法我们按照最大似然概率直接将第一轮估计为硬币2，此时我们更加严谨，只说有0.14的概率是硬币1，有0.86的概率是硬币2。这样我们在估计P1或者P2时，就可以用上全部的数据，而不是部分的数据。此步我们实际上是估计出z的概率分布，称为E步。

按照期望最大似然概率的法则来估计出新的P1和P2。以P1估计为例，第一轮的3正2反相当于有0.14×3=0.42的概率为正，有0.14×2的概率为反。然后依次计算出其他四轮。那么我们可以得到P1概率，可以看到改变了z的估计方法后，新估计出的P1要更加接近0.4，原因是我们使用了所有抛掷的数据，而不是部分的数据。此步中我们根据E步中求出z的概率分布，依据最大似然概率法则去估计P1和P2，称为M步。

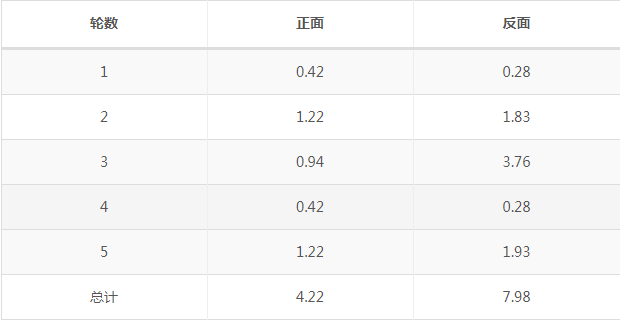
上面我们是通过迭代来得到P1和P2，结果更接近真实的P1和P2。

EM算法推导

Jensen不等式

Jensen不等式表述如下：

如果f是凸函数，x是随机变量，那么：$E[f(x)]\geq f(E[x])$ ,特别地，如果f是严格凸函数，那么当且仅当$P(x=E[x])=1$(也就是说x是常量)，$E[f(x)]=f(E[x])$

通过下面这张图，我们可以加深理解：

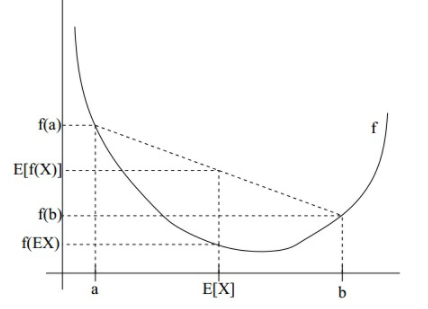
上图中，函数f是凸函数，X是随机变量，有0.5的概率为a，有0.5的概率是b（就像抛硬币一样）。X的期望值就是a和b的中值了，图中可以看到$E[f(x)]\geq f(E[x])$成立.

极大似然估计

EM算法推导过程中，会使用到极大似然估计参数。

极大似然估计是一种概率论在统计学的应用。已知某个随机样本满足某种概率分布，但是其中具体的参数不清楚，参数估计就是通过若干次试验，观察结果，利用结果推出参数的大概值。极大似然估计建立在这样的思想上：已知某个参数能使这个样本出现的概率最大，我们当然不会再去选择其他小概率的样本，所以干脆就把这个参数作为估计的真实值。

这里再给出求极大似然估计值的一般步骤：

  • 1）写出似然函数；
  • 2）对似然函数取对数，并整理；
  • 3）求导数，令导数为0，得到似然方程；
  • 4）解似然方程，得到的参数即为所求；

EM算法推导

对于m个样本观察数据$x=(x^{(1)},x^{(2)},x^{(3)},…,x^{(m)})$，找出样本的模型参数θ，极大化模型分布的对数似然函数如下所示

如果我们得到的观察数据有未观察到的隐含数据$z=(z^{(1)},z^{(2)},z^{(3)},…,z^{(m)})$，此时我们极大化模型分布的对数似然函数如下

上面方程是无法直接求出θ的，因此需要一些特殊技巧，在此我们引入Jensen不等式。

我们再回到上述推导过程，得到如下方程式。

我们来解释下怎样得到的方程式(1)和方程式(2)，上面(1)式中引入一个未知的新的分布$Q_i(z^{(i)})$，第二式用到Jensen不等式。

首先log函数是凹函数，那么E[f(X)]≤f(E[X])，也就是f(E(X))≥E(f(X))。其中$\sum _{z^{(i)}}Q_i(z^{(i)})\frac{P(x^{(i)},z^{(i)};\theta) }{Q_i(z^{(i)})}$ 是$\frac{P(x^{(i)},z^{(i);\theta})}{Q_i(z^{(i)})}$的数学期望，那么$log\sum _{z^{(i)}}Q_i(z^{(i)})\frac{P(x^{(i)},z^{(i)};\theta) }{Q_i(z^{(i)})}$ 便相当于f(E(X))，同时$\sum _{z^{(i)}}Q_i(z^{(i)})log\frac{P(x^{(i)},z^{(i)};\theta) }{Q_i(z^{(i)})}$相当于E(f(X))，因此我们便得到上述方程式(1)(2)。

如果要满足Jensen不等式的等号，那么需要满足X为常量，即为

那么稍加改变能够得到

因此得到下列方程，其中方程(3)利用到条件概率公式。

如果$Q_i(z^{(i)})=P(z^{(i)}|x^{(i)};\theta)$ 那么第(2)式就是我们隐藏数据的对数似然的下界。如果我们能极大化方程式(2)的下界，则也在尝试极大化我们的方程式(1)。即我们需要最大化下式

去掉上式中常数部分，则我们需要极大化的对数似然下界为

注意到上式中$Q_i(z^{(i)})$ 是一个分布，因此$\sum _{z^{(i)}}Q_i(z^{(i)})log P(x^{(i)},z^{(i)};\theta)$ 可以理解为$logP(x^{(i)},z^{(i)};\theta)$ 基于条件概率分布$Q_i(z^{(i)})$的期望，也就是我们EM算法中E步。极大化方程式(4)也就是我们EM算法中的M步。

到这里，我们推出了在固定参数θ后，使下界拉升的Q(z)的计算公式就是后验概率（条件概率），解决了Q(z)如何选择的问题。此步就是EM算法的E步，目的是建立L(θ)的下界。接下来的M步，目的是在给定Q(z)后，调整θ，从而极大化L(θ)的下界J（在固定Q(z)后，下界还可以调整的更大）。那么一般的EM算法的步骤如下：

  • 第一步：初始化分布参数θ；

  • 第二步：重复E步和M步直到收敛：

    E步：根据参数的初始值或上一次迭代的模型参数来计算出的因变量的后验概率（条件概率），其实就是隐变量的期望值，来作为隐变量的当前估计值：

    M步：最大化似然函数从而获得新的参数值：

EM算法可以保证收敛到一个稳定点，但是却不能保证收敛到全局的极大值点，因此它是局部最优的算法。当然，如果我们的优化目标L(θ,θj)是凸的，则EM算法可以保证收敛到全局最大值，这点和梯度下降法中迭代算法相同。

Sklearn实现EM算法

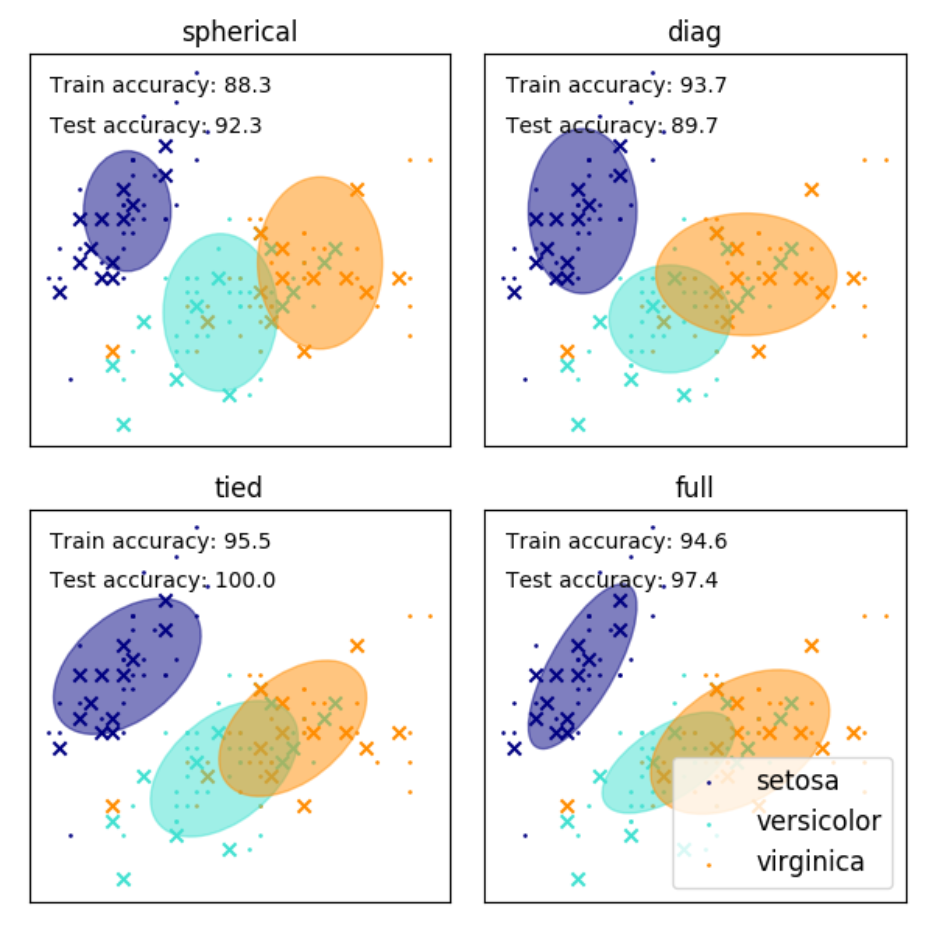
高斯混合模型(GMM)使用高斯分布作为参数模型，利用期望最大(EM)算法进行训练，有兴趣了解高斯混合模型的同学可以去这儿。下列代码来自于Sklearn官网GMM模块，利用高斯混合模型确定iris聚类。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
import matplotlib as mpl
import matplotlib.pyplot as plt

import numpy as np

from sklearn import datasets
from sklearn.mixture import GaussianMixture
from sklearn.model_selection import StratifiedKFold

colors = ['navy', 'turquoise', 'darkorange']

def make_ellipses(gmm, ax):
    for n, color in enumerate(colors):
        if gmm.covariance_type == 'full':
            covariances = gmm.covariances_[n][:2, :2]
        elif gmm.covariance_type == 'tied':
            covariances = gmm.covariances_[:2, :2]
        elif gmm.covariance_type == 'diag':
            covariances = np.diag(gmm.covariances_[n][:2])
        elif gmm.covariance_type == 'spherical':
            covariances = np.eye(gmm.means_.shape[1]) * gmm.covariances_[n]
        v, w = np.linalg.eigh(covariances)
        u = w[0] / np.linalg.norm(w[0])
        angle = np.arctan2(u[1], u[0])
        angle = 180 * angle / np.pi  # convert to degrees
        v = 2. * np.sqrt(2.) * np.sqrt(v)
        ell = mpl.patches.Ellipse(gmm.means_[n, :2], v[0], v[1],
                                  180 + angle, color=color)
        ell.set_clip_box(ax.bbox)
        ell.set_alpha(0.5)
        ax.add_artist(ell)

iris = datasets.load_iris()

# Break up the dataset into non-overlapping training (75%)
# and testing (25%) sets.
skf = StratifiedKFold(n_splits=4)
# Only take the first fold.
train_index, test_index = next(iter(skf.split(iris.data, iris.target)))


X_train = iris.data[train_index]
y_train = iris.target[train_index]
X_test = iris.data[test_index]
y_test = iris.target[test_index]

n_classes = len(np.unique(y_train))

# Try GMMs using different types of covariances.
estimators = dict((cov_type, GaussianMixture(n_components=n_classes,
                   covariance_type=cov_type, max_iter=20, random_state=0))
                  for cov_type in ['spherical', 'diag', 'tied', 'full'])

n_estimators = len(estimators)

plt.figure(figsize=(3 * n_estimators // 2, 6))
plt.subplots_adjust(bottom=.01, top=0.95, hspace=.15, wspace=.05,
                    left=.01, right=.99)


for index, (name, estimator) in enumerate(estimators.items()):
    # Since we have class labels for the training data, we can
    # initialize the GMM parameters in a supervised manner.
    estimator.means_init = np.array([X_train[y_train == i].mean(axis=0)
                                    for i in range(n_classes)])

    # Train the other parameters using the EM algorithm.
    estimator.fit(X_train)

    h = plt.subplot(2, n_estimators // 2, index + 1)
    make_ellipses(estimator, h)

    for n, color in enumerate(colors):
        data = iris.data[iris.target == n]
        plt.scatter(data[:, 0], data[:, 1], s=0.8, color=color,
                    label=iris.target_names[n])
    # Plot the test data with crosses
    for n, color in enumerate(colors):
        data = X_test[y_test == n]
        plt.scatter(data[:, 0], data[:, 1], marker='x', color=color)

    y_train_pred = estimator.predict(X_train)
    train_accuracy = np.mean(y_train_pred.ravel() == y_train.ravel()) * 100
    plt.text(0.05, 0.9, 'Train accuracy: %.1f' % train_accuracy,
             transform=h.transAxes)

    y_test_pred = estimator.predict(X_test)
    test_accuracy = np.mean(y_test_pred.ravel() == y_test.ravel()) * 100
    plt.text(0.05, 0.8, 'Test accuracy: %.1f' % test_accuracy,
             transform=h.transAxes)

    plt.xticks(())
    plt.yticks(())
    plt.title(name)

plt.legend(scatterpoints=1, loc='lower right', prop=dict(size=12))
plt.show()

EM算法优缺点

优点

  • 聚类。
  • 算法计算结果稳定、准确。
  • EM算法自收敛，既不需要事先设定类别，也不需要数据间的两两比较合并等操作。

缺点

  • 对初始化数据敏感。
  • EM算法计算复杂，收敛较慢，不适于大规模数据集和高维数据。
  • 当所要优化的函数不是凸函数时，EM算法容易给出局部最优解，而不是全局最优解。
-------------Thanks for Reading!-------------