朴素贝叶斯

发表于 | 分类于
字数统计: 3.5k | 阅读时长 ≈ 15

注：这篇文章原文出处放在了下面的连接，原文已经写得非常清晰明了，这里有适当的修改和增加内容，写在这里是为了更好地查阅巩固。

戳我原文

朴素贝叶斯（Naive Bayes）是基于贝叶斯定理与特征条件假设的分类方法。

对于给定的训练数据集，首先基于特征条件独立假设学习输入、输出的联合分布；然后基于此模型，对给定的输入x，利用贝叶斯定理求出后验概率最大的输出y。

朴素贝叶斯实现简单，学习与预测的效率都很高，是一种常用的方法。

朴素贝叶斯的学习与分类

贝叶斯定理

先看什么是条件概率

P(A|B)表示事件B已经发生的前提下，事件A发生的概率，叫做事件B发生下事件A的条件概率。其基本求解公式为

贝叶斯定理便是基于条件概率，通过P(A|B)来求P(B|A)：

顺便提一下，上式中的分母，可以根据全概率公式分解为：

特征条件独立假设

这一部分开始朴素贝叶斯的理论推导，从中你会深刻地理解什么是特征条件独立假设。

给定训练数据集(X,Y)，其中每个样本X都包括nn维特征，即$x=(x_1,x_2,···,x_n)$，类标记集合含有K种类别，即$y=(y_1,y_2,···,y_k)$

如果现在来了一个新样本x我们要怎么判断它的类别?从概率的角度来看，这个问题就是给定x，它属于哪个类别的概率更大。那么问题就转化为求解$P(y_1|x),P(y_2|x),P(y_k|x)$中最大的那个，即求后验概率最大的输出：$arg\underset{y_k}{\max}P\left(y_k|x\right)$ 。那$P(y_k|x)$怎么求解？答案就是贝叶斯定理

根据全概率公式，可以进一步分解上式中的分母：

先不管分母，分子中的$P(y_k)$是先验概率，根据训练集就可以简单地计算出来，而条件概率$P(x|y_k)=P(x_1,x_2,···,x_n|y_k)$它的参数规模是指数数量级别的，假设第$i$维特征$x_i$可取值的个数有$S_i$个，类别取值个数为k个，那么参数个数为$k\prod_{j=1}^n{S_j}$

这显然是不可行的。针对这个问题，朴素贝叶斯算法对条件概率分布做了独立性的假设，通俗地讲就是说假设各个维度的特征 $x_1,x_2,···,x_n$互相独立，由于这是一个较强的假设，朴素贝叶斯算法也因此得名。在这个假设的前提上，条件概率可以转化为：

这样参数规模就降到了$\sum_{i=1}^n{S_ik}$

以上就是针对条件概率所作出的特征条件独立性假设，至此，先验概率$P(y_k)$和条件概率$P(x|y_k)$的求解问题就都解决了，那么我们是不是可以求解我们所需要的后验概率$P(y_k|x)$了？

答案是肯定的。我们继续上面关于$P(y_k|x)$的推导，将公式2代入公式1中得到：

于是朴素贝叶斯分类器可表示为：

因为对于所有的$y_k$，上式中的分母的值都是一样的（为什么？注意到全加符号就容易理解了），所以可以忽略分母部分，朴素贝叶斯分裂期最终表示为：

朴素贝叶斯法的参数估计

极大似然估计

根据上述，可知朴素贝叶斯要学习的东西就是$P(Y=c_k)$和$P(X^{j}=a_{jl}|Y=c_k)$可以应用极大似然估计法估计相应的概率（简单讲，就是用样本来推断模型的参数，或者说是使得似然函数最大的参数）

先验概率$P(Y=c_k)$的极大似然估计是

也就是用样本中$c_k$的出现次数除以样本容量。

设第$j$个特征$x^{(j)}$可能取值的集合为${a_{j1},a_{j2},···,a_{jl}}$，条件概率 $P(X^{j}=a_{jl}|Y=c_k)$的极大似然估计是：

式中，$x_i^j$是第$i$个样本的第$j$个特征。

一个例题

例题如下

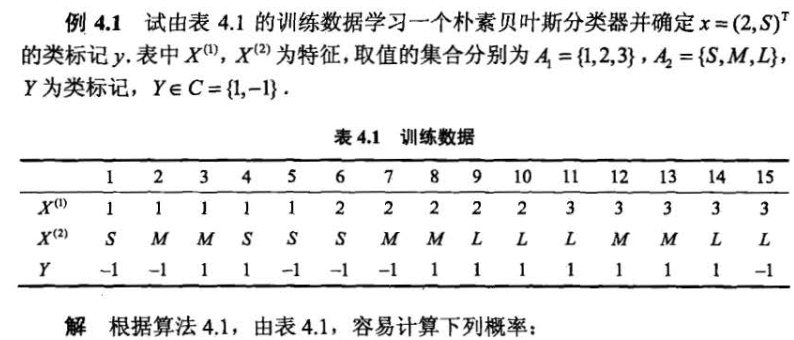
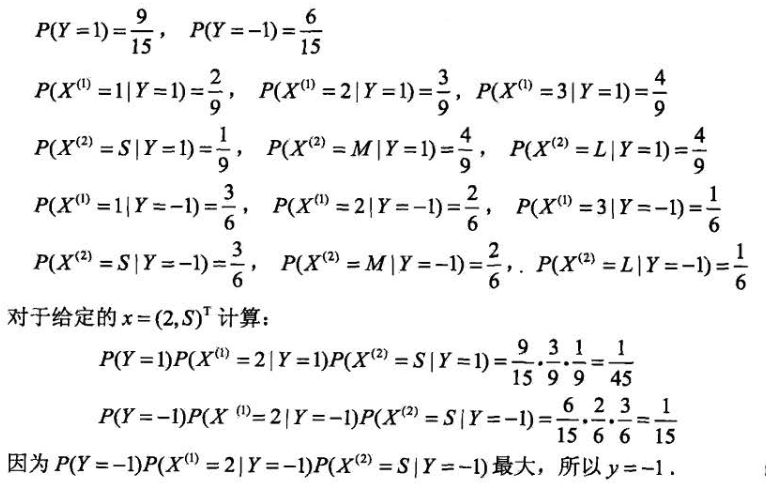
贝叶斯估计

极大似然估计有一个隐患，假设训练数据中没有出现某种参数与类别的组合怎么办？比如上例中当Y=1对应的$X^{(1)}$的取值只有1和2。这样可能会出现所要估计的概率值为0的情况，但是这不代表真实数据中就没有这样的组合。这时会影响到后验概率的计算结果，使分类产生偏差。解决办法是贝叶斯估计。

条件概率的贝叶斯估计：

其中$\lambda≥0$，$S_j$表示第$x_j$个特征可能取值的个数。分子和分母分别比极大似然估计多了一点东西，其意义为在随机变量各个取值的频数上赋予一个正数$λ≥0$。当$λ=0$时就是极大似然估计。常取$λ=1$，这时称为拉普拉斯平滑。

先验概率的贝叶斯估计：（K为类别个数）

例题如下：套入公式计算即可

上诉说的是$X_j$为普通离散型的情况。如果$X_j$是稀疏的离散值，即各个特征的出现概率很低，那么可以假设$X_j$服从伯努利分布，即特征$X_j$出现记为1，不出现记为0。即我们只关注$X_j$是否出现，不关注$X_j$出现的次数，这样得到的$P\left(X^{\left(j\right)}=a_{jl}|Y=c_k\right)$是在是在样本类别$c_k$中$a_{jl}$出现的频率，公式如下所示。其中$a_{jl}$取值为0和1。

如果$X_j$是连续值，那么假设$X_j$的先验概率为高斯分布(正态分布)，这样假设$P\left(X^{\left(j\right)}=a_{jl}|Y=c_k\right)$的概率分布公式如下所示。其中$\mu_k$和$\sigma_{k}^2$是正态分布的期望和方差，$\mu_k$为样本类别$C_k$中，所有$X_j$的平均值，$\sigma_{k}^2$为样本类别$C_k$中，所有$X_j$的方差，$\mu_k$和$\sigma_{k}^2$可以通过极大似然估计求得。

python代码实现

朴素贝叶斯文档分类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
# -*- coding: utf-8 -*-
"""
Created on 下午5:28 22 03 2017
bayes algorithm: classify a words as good or bad   [text classify]
@author: plushunter
"""
from numpy import *
class Naive_Bayes:
    def __init__(self):
        self._creteria = "NB"
    #创建不重复词集
    def _creatVocabList(self,dataSet):
        vocabSet = set([])  # 创建一个空的SET
        for document in dataSet:
            vocabSet = vocabSet | set(document)  # 并集
        return list(vocabSet)  # 返回不重复词表（SET的特性）
    #文档词集向量模型
    def _setOfWordToVec(self,vocabList, inputSet):
        """
        功能:给定一行词向量inputSet，将其映射至词库向量vocabList，出现则标记为1，否则标记为0.
        """
        returnVec = [0] * len(vocabList)
        for word in inputSet:
            if word in vocabList:
                returnVec[vocabList.index(word)] = 1
        return returnVec
    #文档词袋模型
    def _bagOfsetOfWordToVec(self,vocabList, inputSet):
        """
        功能：对每行词使用第二种统计策略，统计单个词的个数，然后映射到此库中
        输出：一个n维向量，n为词库的长度，每个取值为单词出现的次数
        """
        returnVec = [0] * len(vocabList)
        for word in inputSet:
            if word in vocabList:
                returnVec[vocabList.index(word)] += 1 #更新此处代码
        return returnVec
    def _trainNB0(self,trainMatrix, trainCategory):
        """
        输入：训练词矩阵trainMatrix与类别标签trainCategory,格式为Numpy矩阵格式
        功能：计算条件概率p0Vect、p1Vect和类标签概率pAbusive
        """
        numTrainDocs = len(trainMatrix)#样本个数
        numWords = len(trainMatrix[0])#特征个数，此处为词库长度
        pAbusive = sum(trainCategory) / float(numTrainDocs)#计算负样本出现概率（先验概率）
        p0Num = ones(numWords)#初始词的出现次数为1，以防条件概率为0，影响结果
        p1Num = ones(numWords)#同上
        p0Denom = 2.0#类标记为2，使用拉普拉斯平滑法,
        p1Denom = 2.0
        #按类标记进行聚合各个词向量
        for i in range(numTrainDocs):
            if trainCategory[i] == 0:
                p0Num += trainMatrix[i]
                p0Denom += sum(trainMatrix[i])
            else:
                p1Num += trainMatrix[i]
                p1Denom += sum(trainMatrix[i])
        p1Vect = log(p1Num / p1Denom)#计算给定类标记下，词库中出现某个单词的概率
        p0Vect = log(p0Num / p0Denom)#取log对数，防止条件概率乘积过小而发生下溢
        return p0Vect, p1Vect, pAbusive
    def _classifyNB(self,vec2Classify, p0Vec, p1Vec, pClass1):
        """
        该算法包含四个输入:
        vec2Classify表示待分类的样本在词库中的映射集合，
        p0Vec表示条件概率P(wi|c=0)P(wi|c=0)，
        p1Vec表示条件概率P(wi|c=1)P(wi|c=1)，
        pClass1表示类标签为1时的概率P(c=1)P(c=1)。
        p1=ln[p(w1|c=1)p(w2|c=1)…p(wn|c=1)p(c=1)]
        p0=ln[p(w1|c=0)p(w2|c=0)…p(wn|c=0)p(c=0)]
        log取对数为防止向下溢出
        功能:使用朴素贝叶斯进行分类,返回结果为0/1
        """
        p1 = sum(vec2Classify * p1Vec) + log(pClass1)
        p0 = sum(vec2Classify * p0Vec) + log(1 - pClass1)
        if p1 > p0:
            return 1
        else:
            return 0
    #test
    def testingNB(self,testSample):
        "step1：加载数据集与类标号"
        listOPosts, listClasses = loadDataSet()
        "step2：创建词库"
        vocabList = self._creatVocabList(listOPosts)
        "step3：计算每个样本在词库中出现的情况"
        trainMat = []
        for postinDoc in listOPosts:
            trainMat.append(self._bagOfsetOfWordToVec(vocabList, postinDoc))
        p0V, p1V, pAb = self._trainNB0(trainMat, listClasses)
        "step4：测试"
        thisDoc = array(self._bagOfsetOfWordToVec(vocabList, testSample))
        result=self._classifyNB(thisDoc, p0V, p1V, pAb)
        print testSample, 'classified as:', result
        # return result
###
# 加载数据集
def loadDataSet():
    postingList = [['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
                   ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
                   ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
                   ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
                   ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
                   ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
    classVec = [0, 1, 0, 1, 0, 1]  # 1 is abusive, 0 not
    return postingList, classVec
#测试
if __name__=="__main__":
    clf = Naive_Bayes()
    testEntry = [['love', 'my', 'girl', 'friend'],
                 ['stupid', 'garbage'],
                 ['Haha', 'I', 'really', "Love", "You"],
                 ['This', 'is', "my", "dog"],
                 ['maybe','stupid','worthless']]
    for item in testEntry:
        clf.testingNB(item)

使用朴素贝叶斯过滤垃圾邮件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
# -*- coding: utf-8 -*-
"""
Created on 下午8:47 22 03 2017
Email_Classify 
@author: plushunter 
"""
import re
import Bayes
from numpy import *
# mysent='This book is the best book on Python or M.L I have ever laid eyes upon.'
# regEx = re.compile('\\W*')
# listOfTokens=regEx.split(mysent)
# tok=[tok.upper() for tok in listOfTokens if len(tok)>0]
# print tok
#
# emailText=open('email/ham/6.txt').read()
# listOfTokens=regEx.split(emailText)
# print listOfTokens
def textParse(bigString):
    import re
    listOfTokens=re.split(r'\w*',bigString)
    return [tok.lower() for tok in listOfTokens if len(tok)>2]
def spamTest():
    clf = Bayes.Naive_Bayes()
    docList=[]
    classList=[]
    fullText=[]
    for i in range(1,26):
        wordList=textParse(open('email/spam/%d.txt'%i).read())
        docList.append(wordList)
        fullText.extend(wordList)
        classList.append(1)
        wordList=textParse(open('email/ham/%i.txt'%i).read())
        docList.append(wordList)
        fullText.extend(wordList)
        classList.append(0)
    vocabList=clf._creatVocabList(docList)
    trainingSet=range(50);testSet=[]
    for i in range(10):
        randIndex=int(random.uniform(0,len(trainingSet)))
        testSet.append(trainingSet[randIndex])
        del(trainingSet[randIndex])
    trainMatix=[];trainClasses=[]
    for docIndex in trainingSet:
        trainMatix.append(clf._bagOfsetOfWordToVec(vocabList,docList[docIndex]))
        trainClasses.append(classList[docIndex])
    p0V,p1V,pSpam=clf._trainNB0(array(trainMatix),array(trainClasses))
    errorCount = 0
    for docIndex in testSet:
        wordVector = clf._bagOfsetOfWordToVec(vocabList,docList[docIndex])
        if clf._classifyNB(array(wordVector), p0V, p1V, pSpam)!=classList[docIndex]:
            errorCount+=1
    print 'the error rate is :',float(errorCount)/len(testSet)

朴素贝叶斯优缺点

优点

  • 具有稳定的分类效率。
  • 对缺失数据不敏感，算法也比较简单。
  • 对小规模数据表现良好，能处理多分类任务，适合增量式训练。尤其是数据量超出内存后，我们可以一批批的去增量训练。

缺点

  • 对输入数据的表达形式比较敏感，需针对不同类型数据采用不同模型。
  • 由于我们是使用数据加先验概率预测后验概率，所以分类决策存在一定的错误率。
  • 假设各特征之间相互独立，但实际生活中往往不成立，因此对特征个数比较多或特征之间相关性比较大的数据来说，分类效果可能不是太好。
-------------Thanks for Reading!-------------