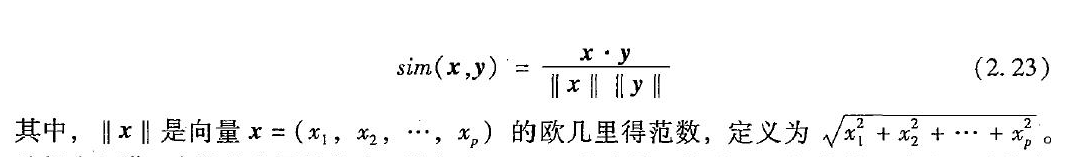数据的基本统计描述
中心趋势度量:均值、中位数和众数
尽管均值是描述数据集的最有用的单个量,但是它并非总是度量数据中心的最佳方法。主要问题是,均值对极端值(例如、离群点)很敏感。为了解决这个问题,我们可以采用结尾均值。结尾均值是丢弃高低极端值后的均值。
对于倾斜(非对称)数据,数据中心的更好的度量是中位数。
度量数据散布:极差、四分位数、方差、标准差和四分位数极差
极差:集合的最大值减去最小值
四分位数第1个四分位数记作$Q_1$,是第25个百分位数,第2个为50%,第3个四分位数记作$Q_3$,第75个百分位数。其中,第1个和第3个百分位数之间的距离是散布的一种简单度量,它给出被数据的中间一半所覆盖的范围。该距离称为四分位数极差(IQR),定义为
识别离群点的通常规则是,挑选落在第3个四分位数之上或第1个四分位数之下至少1.5×IQR处的值。
盒图是一种流行的分布的直观表示,盒图表示了五数概括:
- 盒的端点一般在Q1和Q3四分位数上,使得盒的长度是四分位数极差
- 中位数用盒内的线标记
- 盒外的两条线(称为胡须)延伸到集合的最大和最小值
方差和标准差:标准差是方差的平方根,低的标准差表示数据观测趋向于非常靠近均值。
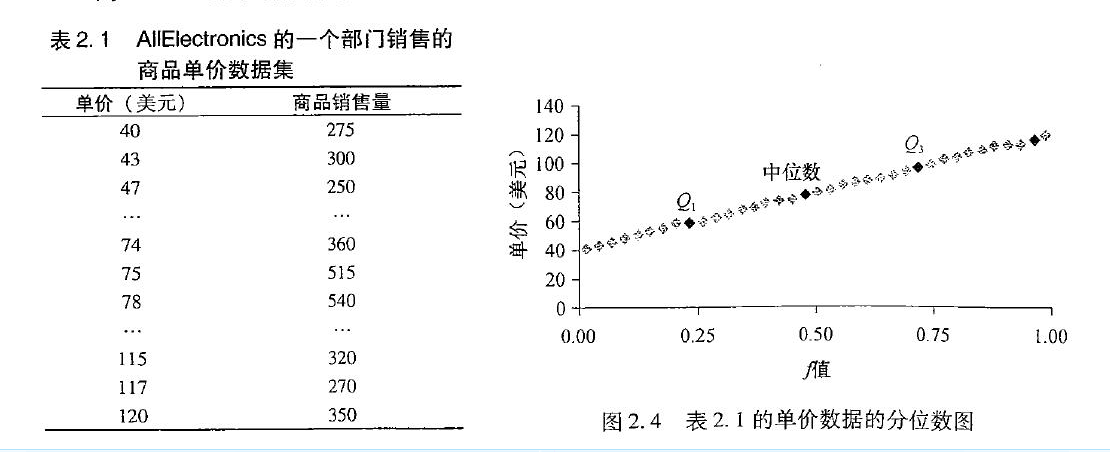
分位数图
分位数图是一种观察数据分布的简单有效的方法。首先,它显示所有的数据(允许用户评估总的情况和不寻常的出现),并将数据由小到大排序,每个观测值$x_(i)$ 与一个百分数 $f_i$ 配对。下图表示了单价数据的分位数图。
分位数-分位数图,或 q-q 图对着另一个的对应分位数,绘制一个单变量分布的分位数。它是一
种强有力的直观表示工具,使得用户可以观察从一个分布到另一个是否有移位。
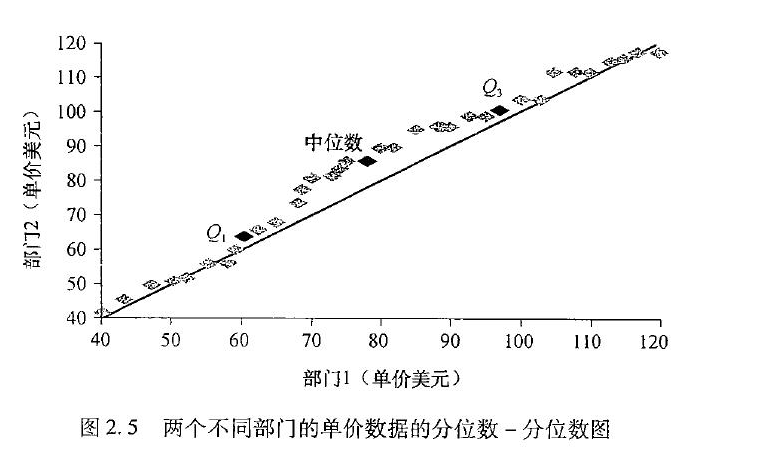
假定对于变量单价,我们有两个观测集,取自两个不同的分店。每组数据都已按递增序排序。下图给出两个部门的QQ图(分位数-分位数图)
度量数据的相似性和相异性
一般的,如果两个对象i和j不相似,则他们的相似性度量将返回0。反之两个对象相似则返回1。
数据矩阵和相异性矩阵
数据矩阵称对象-属性结构,形式为n×p(n个对象p个属性)矩阵存放n个数据对象,每行对应于一个对象;相异性矩阵存放n个对象两两之间的相似度量,是个n×n对称矩阵(类似皮尔逊相关系数)
分类属性的邻近性度量
如何计算分类属性所刻画对象之间的相异性?两个对象i和j之间的相异性可以根据不匹配率来计算:
其中,m是匹配的数目(即i和j取值相同状态的属性数),而p是刻画对象的属性总数。假设我们有表2.2中的4个对象的数据样本,每个对象3个属性,其中只有一个分类属性test-1,在上面的式子中,当对象i和j属性匹配时, $d(i,j)=0$ 当对象不匹配时, $d(i,j)=1$.


布尔属性的邻近性度量
上面表示两个对象的取0或1的属性数目(q,s,r,t)
对于对称的二元属性(布尔属性),是指每个属性都同样重要。基于对称二元属性的相异性称作对称的二元相异性。如果对象i和j都用对称的二元属性刻画,则i和j的相异性为:
互补的,相似性可用下式计算:
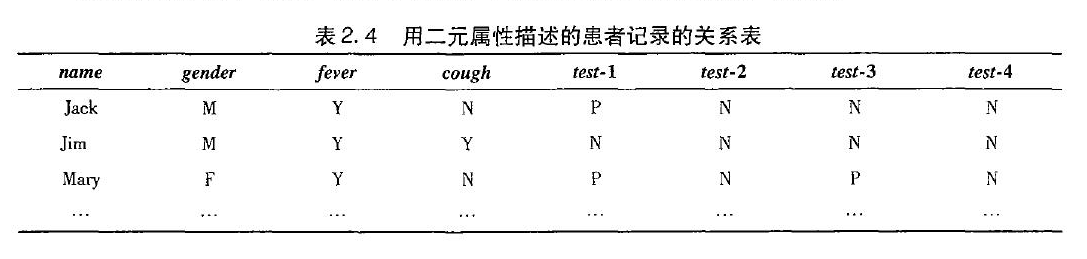
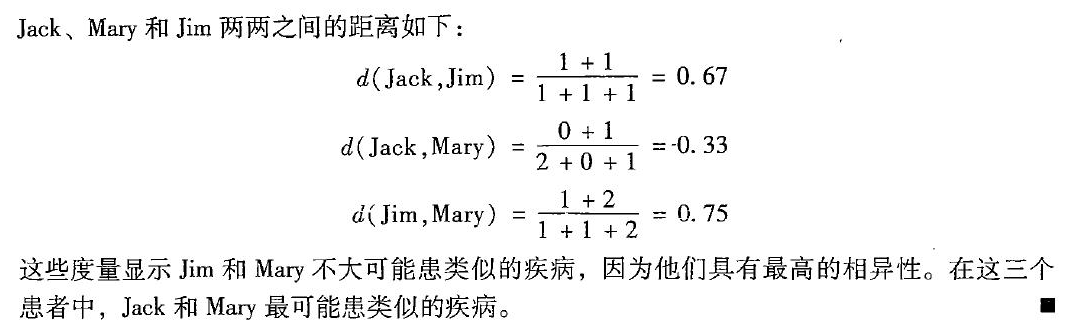
一个例子:下面gender为对称属性,其余为非对称属性(共6个),这里我们只考虑患者(对象)非对称属性,值Y(yes)和P(positive)都设置为1,N(no,negative)为0. 采用上面非对称的二元相异性计算公式。
数值属性的相异性:闵可夫斯基距离
偏序属性的邻近性度量
偏序属性的值之间具有意义的序或排位,例如size属性的序列值[small, medium, large]. 计算这种偏序属性首先计算状态在序数属性上的排名,并映射到[0, 1]数值上。然后把转换后的数值用闵可夫斯基距离来计算相似性。排名转换公式如下:
其中,属性$f$有$M_f$个有序的状态,表示排位$1,2…M_f$。排位$r_{if}$表示当前属性状态排名。
一个例子:

test-2偏序属性,有三个状态,即$M_f$=3,四个对象转换为排位分别为3、1、2、3。然后分别映射为1.0、0.0、0.5、1.0数值,最后可以使用欧几里得距离来计算如下的相异性矩阵。

混合类型属性的相异性
解决这种情况的方法是讲所有类型一起处理,把所有有意义的属性转换到共同区间[0.0 , 1.0]上

1、如果是数值,用归一化。2、如果是类别属性,匹配为1不匹配为0。3、偏序将排位先转为数值,再按数值的归一化处理。
一个例子:(混合了分类、偏序、和数值)

之前,处理test-1(分类属性)和test-2(偏序属性)的过程已经给出,可以使用它们之前的相异性矩阵。所以这里首先计算test-3(数值属性)的相异性矩阵。有max=64,min=22,比较对象用归一化处理后,得到test-3的相异性矩阵:

其中,d(3,1)是对象1和对象3每个不同属性的相似性矩阵计算得到的值,总的处理方式还是归一化。
余弦相似性
给出了四个文档的词频向量,用于比较这些文档之间的相似性。