冗余和相关分析
分类属性的$X^2$卡方检测
对于分类属性,两个属性A和B的相关联系可以通过X2X2(卡方)检测。
以下为一个典型的四格卡方检验,我们想知道喝牛奶对感冒发病率有没有影响:

通过简单的统计我们得出喝牛奶组和不喝牛奶组的感冒率为30.94%和25.00%,两者的差别可能是抽样误差导致,也有可能是牛奶对感冒率真的有影响。
得到的感冒率可能是抽样误差导致,也有可能是牛奶对感冒率真的有影响。
为了确定真实原因,我们先假设喝牛奶对感冒发病率是没有影响的,即喝牛奶喝感冒时独立无关的,所以我们可以得出感冒的实际发病率是(43 + 28)/(43 + 28 + 96 + 84)= 28.29%
所以,理论的四格表应该如下表所示:

即下表:
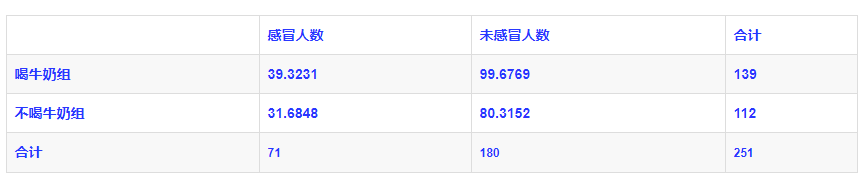
如果喝牛奶喝感冒真的是独立无关的,那么四格表里的理论值和实际值差别应该会很小。
$X^2$卡方检测值可以用下式计算:
其中,A为实际值,T为理论值。$x^2$值用于衡量实际值与理论值的差异程度和相对大小,值越小属性越独立无关,值越大,属性是统计相关的。
根据上面的卡方检验公式,有
卡方分布的临界值:
上一步我们得到了卡方的值,但是如何通过卡方的值来判断喝牛奶和感冒是否真的是独立无关的?也就是说,怎么知道无关性假设是否可靠?
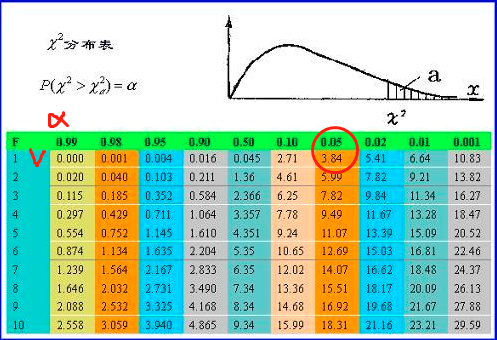
答案是,通过查询卡方分布的临界值表。这里需要用到一个自由度的概念,自由度等于V =(行数- 1)*(列数- 1),对四格表,自由V = 1度。对V = 1,喝牛奶和感概冒95%率不相关的卡方分布的临界概率是:3.84。即如果卡方大于3.84,则认为喝牛奶和感冒有95%的概率相关,有统计联系。
显然1.077 < 3.84,没有达到卡方分布的临界值,所以喝牛奶和感冒独立不相关的假设成立,说明两者之间没说明联系。
数值类型的皮尔逊相关系数
其中,$\bar A$和$\bar B$为均值,和$\sigma_A$ 和$\sigma_B$为标准差。
数值类型的协方差
在概率学和统计学中,协方差和方差是两个类型的度量,评估两个属性如何一起变化。
其中,$E(A\cdot B)$表示期望 ,用均值表示。
协方差值为0表示具有独立性,协方差越大代表两个属性会一起变化。
小波变换
知乎这里讲的很清楚了,主要用于选出有效的特征属性。