这一章很多概念都是之前就接触了,就不一一记录了,这里记录一些感兴趣的吧。
决策树剪枝
为了避免决策树过拟合数据,一般要对决策树进行剪枝:先剪枝和后剪枝
在先剪枝方法中,通过提前停止树的构造(例如,通过决定在给定的结点上不再分裂或划分训练样本的子集)而对树“剪枝”。在构造树时,统计意义下的度量,如信息增益、基尼指数等,可以用于评估分裂的优劣。如果在一个结点划分样本将导致低于预定义阈值的分裂,则给定子集的进一步划分将停止。然而,选取一个适当的阈值是困难的。较高的阈值可能导致过分简化的树,而较低的阈值可能使得树的化简太少。
第二种更常用的方法是后剪枝,它由“完全生长”的树之后再剪去分枝,通过用叶子节点替换要删除的分枝。CART使用的代价复杂度剪枝算法是后剪枝方法的一个实例。该方法把树的复杂度看做树叶节点的个数和树的错误率的函数,如果减去节点N的子树导致较小的代价复杂度,则剪掉该子树;否则,保留该子树。
可伸缩性与决策树
已有的决策树算法,如ID3、C4.5和CART都是为相对较小的数据集规模。另外,大部分情况下,大规模的训练数据不能放在内存!因此,由于训练元组在主存和高速缓存换进换出,决策树的构造可能变得效率低下。最近,已经提出了一些可以解决伸缩问题的决策树算法,例如,RainForest(雨林)能适应可用的内存量,采用了一种新的数据结构形式。
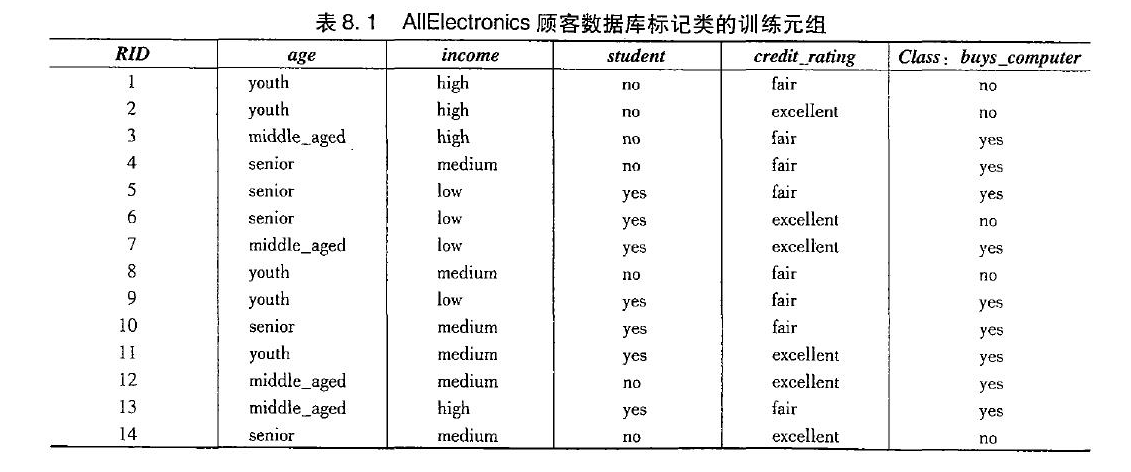
转为AVC集的聚集信息的数据结构来存放
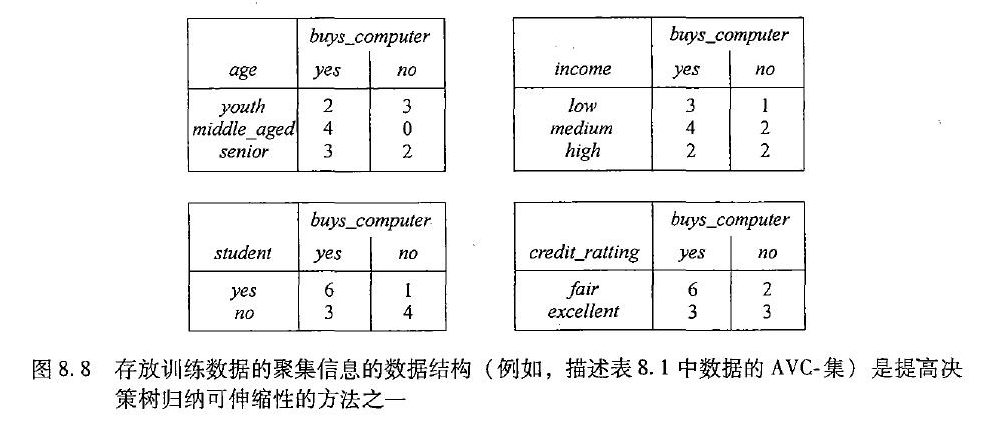
另外一种方法是采用树构造的自助乐观算法(BOAT),它采用了统计学计数,创建给定训练数据的一些较小的样本(或子集),其中每个子集都能放在内存中。使用每个子集构造一颗树,导致多棵树,并使用它们构造一个新树。
使用IF-THEN规则分类
基于规则的分类器使用一组IF-THEN规则进行分类。一个IF-THEN的规则R1一般表示形式有如下两种
1 | R1:IF age=youth AND student=yes THEN buys_conmputer = yes |
规则R可以用覆盖率和准确率来评估。给定类标记的数据集D中的一个元组X,设$n_{covers}$为规则R覆盖的元组数,$n_{covers}$为R正确分类的元组数,|D|是D中的总元组数,可将R的覆盖率和准确率定义为:
如何建立基于规则的分类器呢
- 1、根据决策树提取规则
对从根到树叶节点的每条路经创建一个规则。沿着给定路经上的每个属性-值的逻辑AND形成规则前件(“IF”部分)。叶结点包含类预测,形成规则后件(“THEN”部分)。由于这些规则都是直接从书中提取的,所以它们是互斥的和穷举的(互斥意味不可能存在规则冲突),因此规则的序不重要——它们是无序的。
由于每个树叶对应一个规则,所以提取的规则集的量也很多。所以有两种解决方法,第一种是先对决策树剪枝,然后提取规则。另外一种是直接提取规则,然后修剪规则,对于不能提高规则的估计准确率的任何条件都可以删减,从而泛化该规则。
- 2、使用顺序覆盖算法
顺序覆盖算法是最广泛使用的挖掘分类规则取集的方法,有许多流行的顺序覆盖算法,包括AQ、CN2和最近提出的RIPPER。算法的一般策略如下:一次学习一个规则,每学习一个规则,就删除该规则覆盖的元组,并在剩下的元组上重负该过程。

从最一般的规则开始,即从规则前件条件为空的规则开始。该规则是:
1 | IF THEN loan_decision = accept |
然后,我们考虑每个可以添加到该规则中可能属性测试。Learn_One_Rule采用一种贪心策略,每次选择最能提高规则质量的属性。目前,我们使用规则的准确率作为质量度量。假设Learn_One_Rule发现属性测试income=high最大限度地提高了当前(空)规则的准确率。把它添加到条件中,当前规则变成
1 | IF income=high THEN loan_decision = accept |
下一次迭代时,再次考虑可能的属性测试,结果选中credit_rating=excellent,当前规则增长,变成
1 | IF income=high AND credit_rating=excellent THEN loan_decision = accept |
重复该过程,直到结果规则达到可接受的质量水平。另外,贪心策略如果不自觉选到一个很差的属性怎么办,为了减少这种发生的几率,可以选出最好的k个而不是最好的一个属性添加到当前规则。
规则质量的度量
Learn_One_Rule需要度量规则的质量,之前我们用的是准确率。但准确率本身并非规则质量的可靠估计。这里介绍几个相对有用的几种度量:1)、熵 ;2)、信息增益;3)考虑覆盖率的统计检验
我们想知道给定属性测试到condition中是否导致更好的规则,我们称新的条件为condition’,换言之,我们想知道R’是否比R好。
熵:D是condition’覆盖元组集合,而$p_i$是D中$C_i$类的概率。熵越小,condition’越好。熵更偏向于覆盖单个类大量元组和少量其他类元组的条件。
信息增益:FOIL算法是一种学习一阶逻辑规则的顺序覆盖算法,FOIL用下式估计扩展condition’s而获得信息
它偏向于具有高准确率并且覆盖许多正元组的规则
似然率统计量
其中,m是类数,$f_i$是这些元组类i的观测概率,$e_i$是规则随机预测时类i的期望频率。似然率有助于识别具有显著覆盖率的规则。
CN2使用熵和似然率检验,而FOIL的信息增益被RIPPER使用。
规则剪枝
之前说了可以在决策树生成之后对规则剪枝,有很多剪枝策略。这里介绍FOIL使用的一种简单但很有效的方法,给定规则R,有:
其中,pos和neg分别为规则R覆盖的正元组数和负元组数。这个值将随着R在剪枝集上的准确率增加而增加。因此,如果R剪枝后版本的FOIL_Prune值较高,则对R剪枝。
如何使用规则分类器来预测元组类标号呢?
如果正常的话,R1是唯一满足的规则,则该规则激活,返回X的类预测。但如果有多个规则被触发,它们指定了不同的类,这时则需要一种解决冲突的策略来决定激活哪一个规则。我们考察两种,即规模序和规则序:
规模序:方案吧最高优先权赋予给”最苛刻”要求的规则,其中苛刻性用规则前件的规模度量(类似于树的深度)
规则序:这种序可以是基于类的或基于规则的。使用基于类的序,类按”重要性”递减排序,如按普遍性的降序排序;基于规则的序,或者根据领域专家的建议,把规则组织成一个优先权列表。
使用统计显著性检验选择模型
在前面我们已经使用了 一些策略来测算分类器的准确率(例如K折交叉验证)。在这里,我们假设经处理,最后生成了两个分类器,他们的评估度量都不相同,那么我们应该选择哪个分类器呢?
直观的看法当然是选择指标好的那个分类器呀,但是 实际上这种差别很有可能是偶然的。我们为了判定这种差别是否是偶然的,还需要进行统计显著性检验。 此外,希望得到平均错误率的置信界,使得我们可以做出这样的陈述:”对于未来样本的95%,观测到的均值将不会偏离正、负两个标准差”或者”一个模型比另外一个模型好,误差幅度为±4±4”
这里用的是显著性检验是t-检验。知乎上给出了相关的解释 : 知乎t检验解释 https://www.zhihu.com/question/60321751/answer/399954823
对于10-折交叉验证(k=10)的第ii轮,设$err(M_1)_i$(或$err(M_2)_i$)是模型$M_1$(或$M_2$)在第i轮的错误率。对$M_1$的错误率取平均值得到$M_1$的平均错误率,记为$\overline {err}(M_1)$,类似的,可以得到$\overline {err}(M_2)$。两个模型差的方差记为$var(M_1-M_2)$。在我们的例子中,k=10,这里的k个样本是从每个模型的10-折交叉验证得到的错误率。逐对比较t-统计量按下式计算:
其中
为了计算$M_1$和$M_2$是否显著不同,计算t并选择显著水平sig。实践中,通常使用5%或1%的显著水平。然后,查找t-分布表。通常该表以自由度为行(k个样本具有k-1个自由度,对于我们的例子,自由度为9),显著水平为列。假定要确定$M_1$和$M_2$之间的差对总体的95%(即sig=5%或0.05)是否显著不同。然而,由于t分布是对称的,通常只显示分布上部的百分点,因此,找z=sig/2=0.025的表值,其中z也称为置信界。如果t>z或t<-z,则t落在拒斥域,在分布的尾部。这意味着可以拒绝$M_1$和$M_2$的均值相同的原假设,并断言两个模型之间存在统计的显著的差别。否则,如果不能拒绝原假设,于是断言$M_1$和$M_2$之间的差可能是随机的。
如果有两个检验集而不是单个检验集,则使用t-检验的非逐对版本,其中两个模型的均值之间的方差估计为:
其中,k1和k2分别用于M1和M2的交叉验证样本数(在我们的情况下,10-折交叉验证的轮)。这也称为两个样本的t检验。在查t分布表时,自由度取两个模型的最小自由度。