深度学习（一）：神经网络与反向传播

发表于 | 分类于
字数统计: 5.1k | 阅读时长 ≈ 19

神经元

首先我们从最简单的神经网络——神经元讲起，以下即为一个神经元（Neuron）的图示：

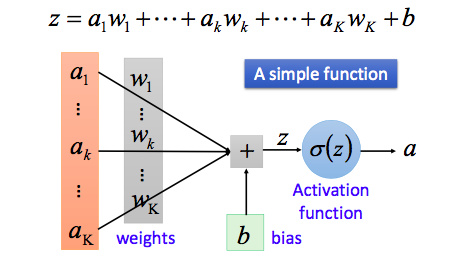
我们知道感知机的激活函数是阶跃函数；而当我们说神经元的时，激活函数往往选择sigmoid函数或tanh函数 ,还有Relu函数（效果较好）。如下图所示

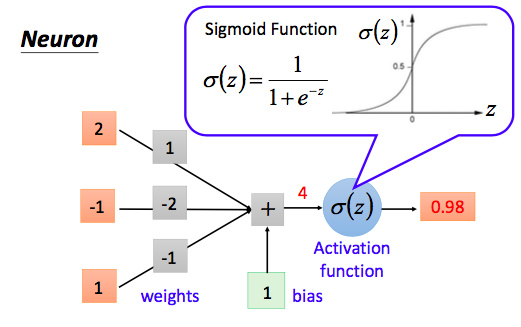
可以看出，这个单一神经元的输入输出的映射关系其实就是一个逻辑回归（logistic regression）。

神经网络模型

神经网络模型

所谓神经网络就是将许多神经元联结在一起，这样，一个神经元的输出就可以是另一神经元的输入。例如，下图就是一个简单的神经网络：

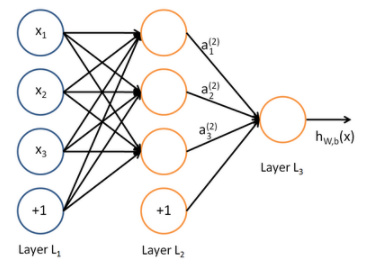
这样的神经网络也称之为多层感知机（MLP），MLP 由一个（通过）输入层、一个或多个称为隐藏层的 LTU （单层感知器）组成，一个最终层 LTU 称为输出层。除了输出层之外的每一层包括偏置神经元，并且全连接到下一层。当人工神经网络有两个或多个隐含层时，称为深度神经网络（DNN）。

BP反向传播

反向传播指的是计算神经⽹络参数梯度的⽅法。总的来说，反向传播依据微积分中的链式法则，沿着从输出层到输⼊层的顺序，依次计算并存储⽬标函数有关神经⽹络各层的中间变量以及参数的梯度。

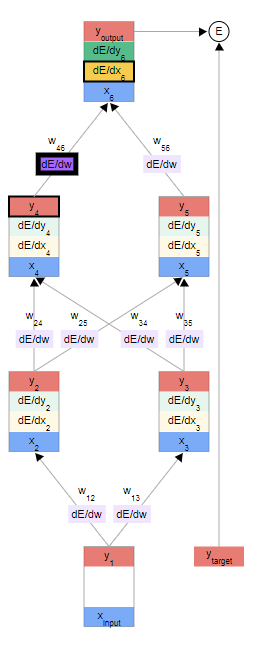
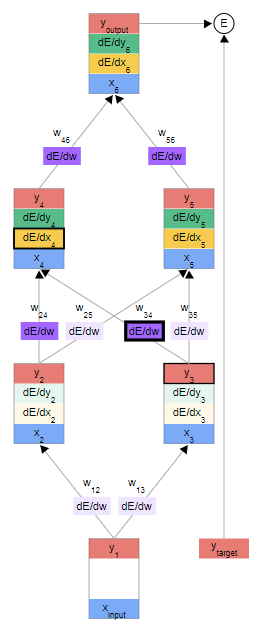
上图依次为利用dE/dx6求出第一个dE/dw; 利用分量的点对点继续求dE/dw; 利用求和来下一个dE/dy2 ;(这里的所以x,y总输入输出都是知道的)

  • dE/dw是有上下夹层dE/dx与上面一层的y求出的
  • dE/dy是由上面一层全连接的wij 与其连接的dE/dx求出的

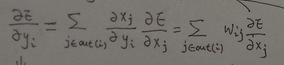
dE/dy2 = dE/dx4, w24 和 dE/dx5, dw25的求和得到其中，y2=w24*x4,故有dx_j/dy_i = wij

用 TensorFlow 高级 API 训练 MLP

与 TensorFlow 一起训练 MLP 最简单的方法是使用高级 API TF.Learn，这与 sklearn 的 API 非常相似。DNNClassifier可以很容易训练具有任意数量隐层的深度神经网络，而 softmax 输出层输出估计的类概率。例如，下面的代码训练两个隐藏层的 DNN（一个具有 300 个神经元，另一个具有 100 个神经元）和一个具有 10 个神经元的 SOFTMax 输出层进行分类：

1
2
3
4
5
import tensorflow as tf
feature_columns = tf.contrib.learn.infer_real_valued_columns_from_input(X) 
dnn_clf = tf.contrib.learn.DNNClassifier(hidden_units=[300, 100], n_classes=10,
                                         feature_columns=feature_columns) 
dnn_clf.fit(x=X, y=y, batch_size=50, steps=40000)

如果你在 MNIST 数据集上运行这个代码（在缩放它之后，例如，通过使用 skLearn 的StandardScaler），你实际上可以得到一个在测试集上达到 98.1% 以上精度的模型！

1
>>> from sklearn.metrics import accuracy_score >>> y_pred = list(dnn_clf.predict(X_test)) >>> accuracy_score(y_test, y_pred) 0.98180000000000001

TF.Learn 学习库也为评估模型提供了一些方便的功能：

1
>>> dnn_clf.evaluate(X_test, y_test) {'accuracy': 0.98180002, 'global_step': 40000, 'loss': 0.073678359}

使用普通 TensorFlow 训练 DNN

如果您想要更好地控制网络架构，您可能更喜欢使用 TensorFlow 的较低级别的 Python API。 在本节中，我们将使用与之前的 API 相同的模型，我们将实施 Minibatch 梯度下降来在 MNIST 数据集上进行训练。 第一步是建设阶段，构建 TensorFlow 图。 第二步是执行阶段，您实际运行计算图谱来训练模型。

构造阶段

开始吧。 首先我们需要导入tensorflow库。 然后我们必须指定输入和输出的数量，并设置每个层中隐藏的神经元数量：

1
import tensorflow as tfn_inputs = 28*28 # MNISTn_hidden1 = 300n_hidden2 = 100n_outputs = 10

接下来，可以使用占位符节点来表示训练数据和目标。X的形状仅有部分被定义。 我们知道它将是一个 2D 张量（即一个矩阵），沿着第一个维度的实例和第二个维度的特征，我们知道特征的数量将是28×28（每像素一个特征） 但是我们不知道每个训练批次将包含多少个实例。 所以X的形状是(None, n_inputs)。 同样，我们知道y将是一个 1D 张量，每个实例有一个入口，但是我们再次不知道在这一点上训练批次的大小，所以形状(None)。

1
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")y = tf.placeholder(tf.int64, shape=(None), name="y")

现在让我们创建一个实际的神经网络。 占位符X将作为输入层; 在执行阶段，它将一次更换一个训练批次（注意训练批中的所有实例将由神经网络同时处理）。 现在您需要创建两个隐藏层和输出层。 两个隐藏的层几乎相同：它们只是它们所连接的输入和它们包含的神经元的数量不同。 输出层也非常相似，但它使用 softmax 激活函数而不是 ReLU 激活函数。 所以让我们创建一个neuron_layer()函数，我们将一次创建一个图层。 它将需要参数来指定输入，神经元数量，激活函数和图层的名称：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def neuron_layer(X, n_neurons, name, activation=None):
    with tf.name_scope(name):
        n_inputs = int(X.get_shape()[1])
        stddev = 2 / np.sqrt(n_inputs)
        init = tf.truncated_normal((n_inputs, n_neurons), stddev=stddev)
        W = tf.Variable(init, name="weights") # 使用满足分布概率来更好第初始化W权重
        b = tf.Variable(tf.zeros([n_neurons]), name="biases")
        # multiply这个函数实现的是元素级别的相乘，也就是两个相乘的数元素各自相乘，而不是矩阵乘法
        # tf.matmul才算矩阵乘法，注意区别
        z = tf.matmul(X, W) + b 
        if activation == "relu":
            return tf.nn.relu(z)
        else:
            return z

我们逐行浏览这个代码：

  1. 首先，我们使用名称范围来创建每层的名称：它将包含该神经元层的所有计算节点。 这是可选的，但如果节点组织良好，则 TensorBoard 图形将会更加出色。
  2. 接下来，我们通过查找输入矩阵的形状并获得第二个维度的大小来获得输入数量（第一个维度用于实例数量）。
  3. 接下来的三行创建一个保存权重矩阵的W变量。 它将是包含每个输入和每个神经元之间的所有连接权重的2D张量；因此，它的形状将是(n_inputs, n_neurons)。它将被随机初始化，使用具有标准差为2/√n的截断的正态（高斯）分布(使用截断的正态分布而不是常规正态分布确保不会有任何大的权重，这可能会减慢训练。).使用这个特定的标准差有助于算法的收敛速度更快（我们将在后面进一步讨论这一点），这是对神经网络的微小调整之一，对它们的效率产生了巨大的影响）。 重要的是为所有隐藏层随机初始化连接权重，以避免梯度下降算法无法中断的任何对称性。（例如，如果将所有权重设置为 0，则所有神经元将输出 0，并且给定隐藏层中的所有神经元的误差梯度将相同。 然后，梯度下降步骤将在每个层中以相同的方式更新所有权重，因此它们将保持相等。 换句话说，尽管每层有数百个神经元，你的模型就像每层只有一个神经元一样。）
  4. 下一行创建一个偏差的b变量，初始化为 0（在这种情况下无对称问题），每个神经元有一个偏置参数。
  5. 然后我们创建一个子图来计算z = X·W + b。 该向量化实现将有效地计算输入的加权和加上层中每个神经元的偏置，对于批次中的所有实例，仅需一次.
  6. 最后，如果激活参数设置为relu，则代码返回relu(z)（即max(0,z)），否则它只返回z。

好了，现在你有一个很好的函数来创建一个神经元层。 让我们用它来创建深层神经网络！ 第一个隐藏层以X为输入。 第二个将第一个隐藏层的输出作为其输入。 最后，输出层将第二个隐藏层的输出作为其输入。

1
2
3
4
with tf.name_scope("dnn"):
        hidden1 = neuron_layer(X, n_hidden1, "hidden1", activation="relu")
    hidden2 = neuron_layer(hidden1, n_hidden2, "hidden2", activation="relu")
    logits = neuron_layer(hidden2, n_outputs, "outputs")

要注意，logit 是在通过 softmax 激活函数之前神经网络的输出：为了优化，我们稍后将处理 softmax 计算。

正如你所期望的，TensorFlow 有许多方便的功能来创建标准的神经网络层，所以通常不需要像我们刚才那样定义你自己的neuron_layer()函数。 例如，TensorFlow 的tf.layers.dense()函数创建一个完全连接的层，其中所有输入都连接到图层中的所有神经元。 它使用正确的初始化策略来负责创建权重和偏置变量，并且默认情况下不使用激活函数（我们可以使用activate_fn参数来更改它）。 它还支持正则化和归一化参数。 我们来调整上面的代码来使用tf.layers.dense()函数，而不是我们的neuron_layer()函数。 只需导入该功能，并使用以下代码替换之前所有 dnn 构建部分：

1
2
3
4
5
6
with tf.name_scope("dnn"):
    hidden1 = tf.layers.dense(X, n_hidden1, name="hidden1",
                              activation=tf.nn.relu)
    hidden2 = tf.layers.dense(hidden1, n_hidden2, name="hidden2",
                              activation=tf.nn.relu)
    logits = tf.layers.dense(hidden2, n_outputs, name="outputs")

损失函数

现在我们已经有了神经网络模型，我们需要定义我们用来训练的损失函数。 正如我们在之前对 Softmax 回归所做的那样，我们将使用交叉熵。 我们将使用sparse_softmax_cross_entropy_with_logits()：它根据“logit”计算交叉熵（即，在通过 softmax 激活函数之前的网络输出），并且期望以 0 到 -1 数量的整数形式的标签（在我们的例子中，从 0 到 9）。 这将给我们一个包含每个实例的交叉熵的 1D 张量。 然后，我们可以使用 TensorFlow 的reduce_mean()函数来计算所有实例的平均交叉熵。

1
2
3
with tf.name_scope("loss"):
    xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
    loss = tf.reduce_mean(xentropy, name="loss")

该sparse_softmax_cross_entropy_with_logits()函数等同于应用 SOFTMAX 激活函数，然后计算交叉熵，但它更高效，它妥善照顾的边界情况下，比如 logits 等于 0，这就是为什么我们没有较早的应用 SOFTMAX 激活函数。 还有称为softmax_cross_entropy_with_logits()的另一个函数，该函数在标签单热载体的形式（而不是整数 0 至类的数目减 1）。

优化器

我们有神经网络模型，我们有损失函数，现在我们需要定义一个GradientDescentOptimizer来调整模型参数以最小化损失函数。没什么新鲜的; 就像我们之前中所做的那样：

1
2
3
4
5
learning_rate = 0.01

with tf.name_scope("train"):
    optimizer = tf.train.GradientDescentOptimizer(learning_rate)
    training_op = optimizer.minimize(loss)

评估模型性能

建模阶段的最后一个重要步骤是指定如何评估模型。 我们将简单地将精度用作我们的绩效指标。 首先，对于每个实例，通过检查最高 logit 是否对应于目标类别来确定神经网络的预测是否正确。 为此，您可以使用in_top_k()函数。 这返回一个充满布尔值的 1D 张量，因此我们需要将这些布尔值转换为浮点数，然后计算平均值。 这将给我们网络的整体准确性.

1
2
3
with tf.name_scope("eval"):
    correct = tf.nn.in_top_k(logits, y, 1)
    accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))

而且，像往常一样，我们需要创建一个初始化所有变量的节点，我们还将创建一个Saver来将我们训练有素的模型参数保存到磁盘中：

1
2
init = tf.global_variables_initializer()
saver = tf.train.Saver()

建模阶段结束。 这是不到 40 行代码，但相当激烈：我们为输入和目标创建占位符，我们创建了一个构建神经元层的函数，我们用它来创建 DNN，我们定义了损失函数，我们 创建了一个优化器，最后定义了性能指标。 现在到执行阶段。

执行阶段

首先，我们加载 MNIST。 我们可以像之前的章节那样使用 ScikitLearn，但是 TensorFlow 提供了自己的助手来获取数据，将其缩放（0 到 1 之间），将它洗牌，并提供一个简单的功能来一次加载一个小批量：

1
2
3
4
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/")
n_epochs = 10001  # 迭代次数
batch_size = 50   # 小批量大小

现在我们去训练模型:

1
2
3
4
5
6
7
8
9
10
11
with tf.Session() as sess:
    init.run()
    for epoch in range(n_epochs):
        for iteration in range(mnist.train.num_examples // batch_size): # 每批量一次
            X_batch, y_batch = mnist.train.next_batch(batch_size)
            sess.run(training_op, feed_dict={X: X_batch, y: y_batch}) # 运行计算程序
        acc_train = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
        acc_test = accuracy.eval(feed_dict={X: mnist.test.images, y: mnist.test.labels})
        print(epoch, "Train accuracy:", acc_train, "Test accuracy:", acc_test)

    save_path = saver.save(sess, "./my_model_final.ckpt")

该代码打开一个 TensorFlow 会话，并运行初始化所有变量的init节点。 然后它运行的主要训练循环：在每个时期，通过一些小批次的对应于训练集的大小的代码进行迭代。 每个小批量通过next_batch()方法获取，然后代码简单地运行训练操作，为当前的小批量输入数据和目标提供。 接下来，在每个时期结束时，代码评估最后一个小批量和完整训练集上的模型，并打印出结果。 最后，模型参数保存到磁盘。

使用神经网络进行预测

现在神经网络被训练了，你可以用它进行预测。 为此，您可以重复使用相同的建模阶段，但是更改执行阶段，如下所示：

1
2
3
4
5
with tf.Session() as sess:
    saver.restore(sess, "./my_model_final.ckpt") # or better, use save_path
    X_new_scaled = mnist.test.images[:20]
    Z = logits.eval(feed_dict={X: X_new_scaled})
    y_pred = np.argmax(Z, axis=1)

首先，代码从磁盘加载模型参数。 然后加载一些您想要分类的新图像。 记住应用与训练数据相同的特征缩放（在这种情况下，将其从 0 缩放到 1）。 然后代码评估对数点节点。 如果您想知道所有估计的类概率，则需要将softmax()函数应用于对数，但如果您只想预测一个类，则可以简单地选择具有最高 logit 值的类（使用argmax()函数做的伎俩）。

微调神经网络超参数

神经网络的灵活性也是其主要缺点之一：有很多超参数要进行调整。 不仅可以使用任何可想象的网络拓扑（如何神经元互连），而且即使在简单的 MLP 中，您可以更改层数，每层神经元数，每层使用的激活函数类型，权重初始化逻辑等等。 你怎么知道什么组合的超参数是最适合你的任务？

可以使用具有交叉验证的网格搜索来查找正确的超参数 ，但是由于要调整许多超参数，并且由于在大型数据集上训练神经网络需要很多时间 。像之前讨论过的，使用随机搜索要好得多 ，另一个选择是使用诸如 Oscar 之类的工具，它可以实现更复杂的算法，以帮助您快速找到一组好的超参数.

隐藏层数量

实际上已经表明，只有一个隐藏层的 MLP 可以建模甚至最复杂的功能，只要它具有足够的神经元。 但是他们忽略了这样一个事实：深层网络具有比浅层网络更高的参数效率：他们可以使用比浅网格更少的神经元来建模复杂的函数，使得训练更快。

总而言之，对于许多问题，您可以从一个或两个隐藏层开始。(MNIST 数据集上容易达到 97% 以上的准确度使用两个具有相同总神经元数量的隐藏层 )；对于更复杂的问题，您可以逐渐增加隐藏层的数量，直到您开始覆盖训练集。 但是，我们很少从头开始训练这样的网络：重用预先训练的最先进的网络执行类似任务的部分更为常见。训练将会更快，需要更少的数据 。

每层隐藏层的神经元数量

不幸的是，正如你所看到的，找到完美的神经元数量仍然是黑色的艺术.

一个更简单的方法是选择一个具有比实际需要的更多层次和神经元的模型，然后使用早期停止来防止它过度拟合（以及其他正则化技术，特别是 drop out，我们将在后面）。 这被称为“拉伸裤”的方法：而不是浪费时间寻找完美匹配您的大小的裤子，只需使用大型伸缩裤，缩小到合适的尺寸。

激活函数

在大多数情况下，您可以在隐藏层中使用 ReLU 激活函数（或其中一个变体 ）

对于输出层，softmax 激活函数通常是分类任务的良好选择（当这些类是互斥的时）。 对于回归任务，您完全可以不使用激活函数。

  1. 为什么通常使用逻辑斯蒂回归分类器而不是经典感知器（即使用感知器训练算法训练单层的线性阈值单元）？你如何调整感知器使之等同于逻辑回归分类器？

答：经典感知器只有在数据集是线性可分的情况下才会收敛。相比之下，逻辑回归分类器将收敛于一个很好的解决方案，即使数据集不是线性可分的，它会输出类的概率。如果你将感知器的激活函数改为逻辑激活函数(或如果有多个神经元，则为softmax激活函数)，，则等价于逻辑回归分类器。

  1. 为什么激活函数是训练第一个 MLP 的关键因素？

答：logistic激活函数是训练第一批MLP的关键因素，因为它是一个复杂的过程导数总是不为零的，所以梯度下降总是可以沿着斜率向下滚动。当激活函数是阶跃函数，梯度下降无法移动，因为根本没有斜率。

  1. 假设有一个 MLP 有一个 10 个神经元组成的输入层，接着是一个 50 个神经元的隐藏层，最后一个 3 个神经元输出层。所有人工神经元使用 Relu 激活函数。
  • 输入矩阵X的形状是什么？ —— -m × 10，其中m为batch size.
  • 隐藏层的权重向量的形状以及它的偏置向量的形状如何？ ——W_h=50 × 10，b_h = 50（一维长度）
  • 输出层的权重向量和它的偏置向量的形状是什么？ ——W_o=50 × 3，b_o=3
  • 网络的输出矩阵Y是什么形状？ ——Y=m × 3
  • 写出计算网络输出矩阵的方程 —$-Y=(X\cdot W_h+b_h)\cdot W_o+b_o$
  1. 如果你想把电子邮件分类成垃圾邮件或正常邮件，你需要在输出层中有多少个神经元？在输出层中应该使用什么样的激活函数？如果你想解决 MNIST 问题，你需要多少神经元在输出层，使用什么激活函数？

答：只需要神经系统在输出层中的一个神经元，通常在估计概率时，使用输出层的logistic激活函数。如果你想处理mnist，你需要输出层的10个神经元，你必须替换
logistic函数与softmax激活函数，它可以处理多个分裂，每个类输出一个概率。如果现在想让你的神经网络预测房屋价格，则需要一个输出神经元，不使用任何激活函数
输出层。

-------------Thanks for Reading!-------------