认识卷积神经网络
全连接神经网络之所以不太适合图像识别任务,主要有三个方面的问题:
- 参数数量太多,一个输入1000×1000像素的图片有100万个神经元(一个像素点代表一个神经元)
- 没有利用像素之间的位置信息
- 网络层数限制,网络层数越多,其表达能力越强,但是通过梯度下降方法训练深度全连接神经网络很困难,因为全连接神经网络的梯度很难传递超过三层。
局部感受野(local receptive fields)
在之前的全连接神经网络中,一个样例的输入被转换为一个一维向量。但在一个卷积网络中,把输入看作是一个按照28×28排列的正方形,或者当有颜色通道的时候,比如28x28x3,就是宽高都是28,且有3个颜色通道。比如下图就代表了一个输入

然后,我们通常把输入像素连接到一个隐藏层的神经元,但和全连接神经网络那样每个输入都连接一个隐藏层神经元不同的是,这里我们只是把输入图像进行局部的连接。
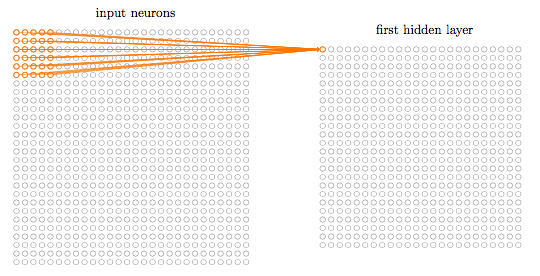
如此不断地重复,构建起第一个隐藏层。注意如果我们有一个28×28的输入图像,5×5的局部感受野,那么隐藏层中就会有24×24个神经元。这是因为在抵达抵达最右边或最底部的输入图像之前,我们只能把局部感受野向右或向下移动23个神经元。
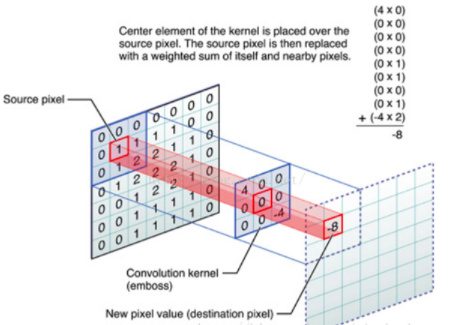
如上图所示,把图中间的那个看作是可以“滑动的窗口”,他的作用是和输入相应的“感受域”下的像素做运算得到新的值。这个运算就是“卷积”运算了。图上面有详细的运算过程。实际上就是每个相应元素的值相乘,然后把得到的都加起来。这个窗口的本质是其中的数字和一个偏置构成的,通常就把这个窗口(Convolution kernel)叫做滤波器或者卷积核(相当于是全连接层里面要求的隐藏权重,它代表识别某个特征)。 这个“窗口”是可以滑动的,每次的滑动步长可以人为指定 。
池化(Pooling)
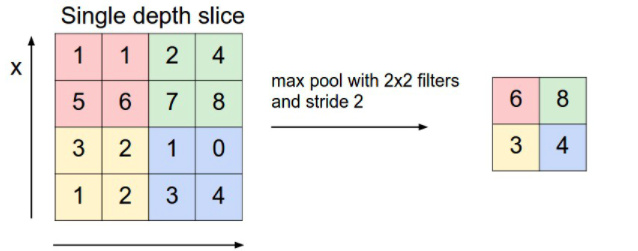
它的作用是逐渐降低数据体的空间尺寸,这样的话就能减少网络中参数的数量,使得计算资源耗费变少,也能有效控制过拟合。最常见的形式是汇聚层使用尺寸2x2的滤波器,以步长为2来对每个深度切片进行降采样,将其中75%的激活信息都丢掉。每个MAX操作是从4个数字中取最大值(也就是在深度切片中某个2x2的区域)。深度保持不变。
Pooling的方法很多,最常用的是Max Pooling。 此外,还有平均池化(average pooling)和L2-norm池化。
卷积神经网络的层
首先,让我们对卷积神经网络有一个感性的认识,下图就是一个卷积神经网络的示意图:
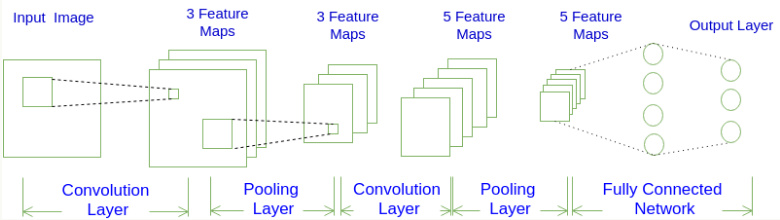
如上图所示,一个神经网络由若干卷积层(CONV)、Pooling层(POOL)、全连接层(FC)组成。你可以构建各种不同的卷积神经网络,它的常用架构模式为:
也就是N个卷积层叠加,然后叠加一个Pooling层(可选),重复这个结构M次,最后叠加K个全连接层。
对于上图来说,该卷积神经网络的架构为:
也就是N=1,M=2,K=2
我们看到输入层的宽度和高度对应于输入图像的宽度和高度,而他的深度为1。接着第一个卷积层对这幅图像进行了卷积操作,得到了三个Feature Map。实际上这个卷积层包含三个Filter(卷积核,是隐藏不显示图上的),也就是三套参数,每个Filter都可以把原始输入图像卷积得到一个Feature Map,三个Filter就可以得到三个Feature Map。至于一个卷积层可以有多少个Filter,那是可以自由设定的。也就是说,卷积层的Filter个数也是一个超参数。我们可以把Feature Map可以看做是通过卷积变换提取到的图像特征,三个Filter就对原始图像提取出三组不同的特征,也就是得到了三个Feature Map,也称做三个通道(channel)。
在第一个卷积层之后,Pooling层对三个Feature Map做了下采样,得到了三个更小的Feature Map。接着,是第二个卷积层,它有5个Filter。每个Fitler都把前面下采样之后的3个Feature Map卷积在一起(每个Fitlter与输入有相同的深度,然后对应相乘后总相加),得到一个新的Feature Map。这样,5个Filter就得到了5个Feature Map。接着,是第二个Pooling,继续对5个Feature Map进行下采样,得到了5个更小的Feature Map。
最后两层是全连接层。第一个全连接层的每个神经元,和上一层5个Feature Map中的每个神经元相连,第二个全连接层(也就是输出层)的每个神经元,则和第一个全连接层的每个神经元相连,这样得到了整个网络的输出。
至此,我们对卷积神经网络有了最基本的感性认识。接下来,我们将介绍卷积神经网络中各种层的计算和训练。
卷积层
卷积层的参数是一些可学习的滤波器(卷积核,隐藏不显示,相当于全连接层的隐藏权重)构成,滤波器的宽度和高度一般不大,深度与其输入数据保持一致。见下图:
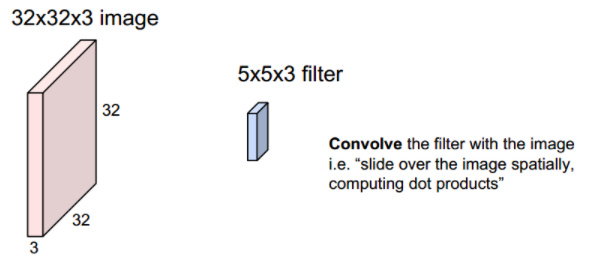
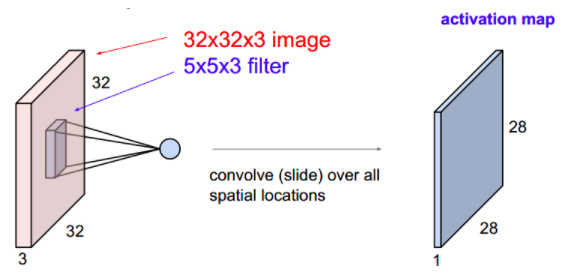

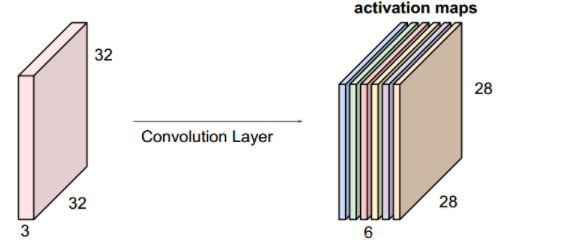
要点:卷积层有一个或多个滤波器(卷积核)构成,每个卷积核宽度和高度(这里为5×5)一般不大,深度(这里为3)与其输入数据保持一致。这里有6个不同的卷积核,得到的6个不同的activation map分别表示诸如边缘特征、形状特征等特征图,将这些activation map映射在深度方向上层叠起来就生成了输出数据。所以在用了6个过滤器(卷积层)之后,我们可以得到28×28×6的激活图。
卷积层输出值的计算
我们使用一个简单的例子来讲述如何计算卷积,然后,抽象出卷积层的一些重要概念和计算方法。
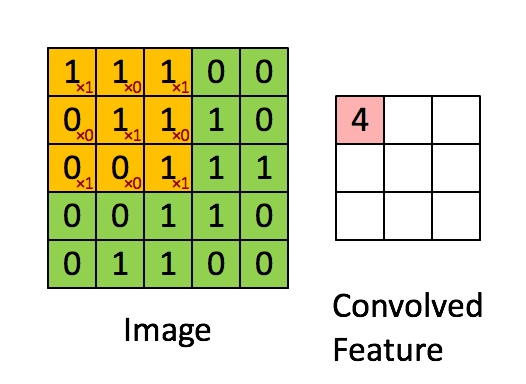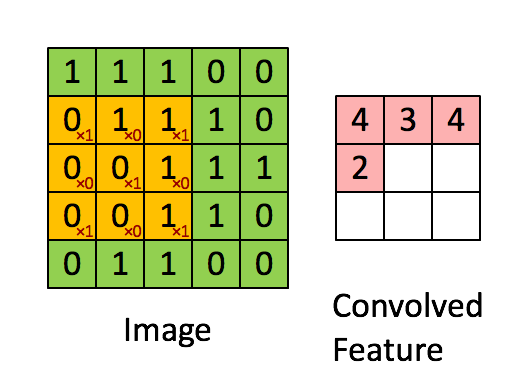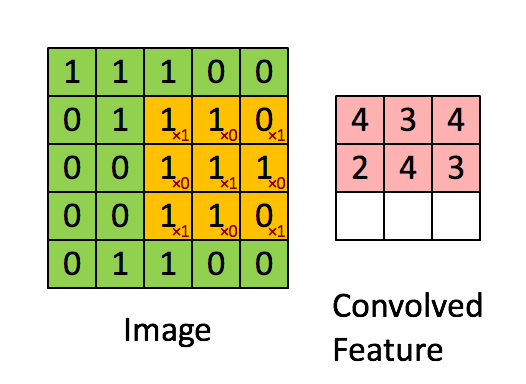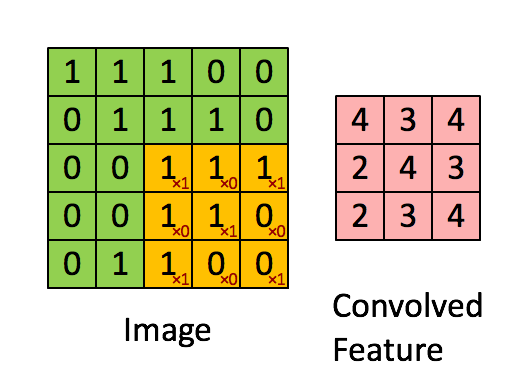
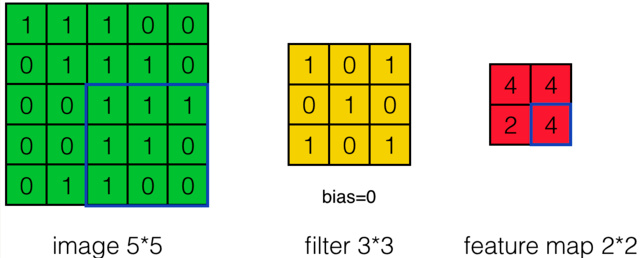
假设有一个5×5的图像,使用一个3×3的滤波器进行卷积,想得到3×3的Feature Map,如下所示:
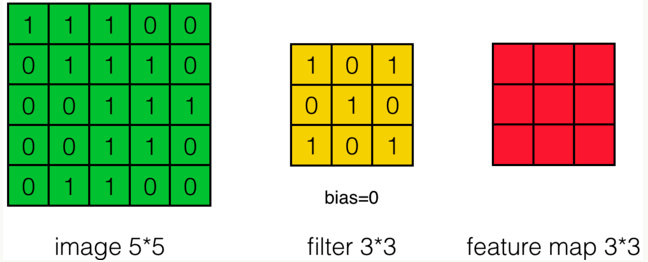
为了清楚地描述卷积的计算过程,我们首先对图像的每个像素进行编号,用$x_{i,j}$表示图像的第i行第j列元素,对filter的每个权重进行编号,用$w_{m,n}$表示第m行第n列权重,用$w_b$表示filter的偏置项;对Feature Map的每个元素进行编号,用$a_{i,j}$表示Feature Map的第i行第j列元素;用f表示激活函数(此处使用Relu函数作为激活函数)。然后使用下列公式计算卷积:
例如,对于Feature Map的左上角元素$a_{0,0}$来说,其卷积计算方法为:
按照这个公式可以依次计算出Feature Map中所有的值,下面的动画显示了整个Feature Map的计算过程:
填充和步幅
假设输入形状的$n_h\times n_w$,卷积核窗口形状是$k_h\times k_w$,那么输出的形状将会是
所以卷积层的输出形状由输⼊形状和卷积核窗口形状决定。这里我们将介绍卷积层的两个超参数,填充和步幅。它们可以对给定形状的输⼊和卷积核改变输出形状。
填充(padding)是指在输入和宽的两侧填充元素(通常是0元素)。下图表示在原输入高的宽的两侧分别添加了值为0的元素,使得高和宽从3变成了5,并导致输出的高和宽由2增加到4.
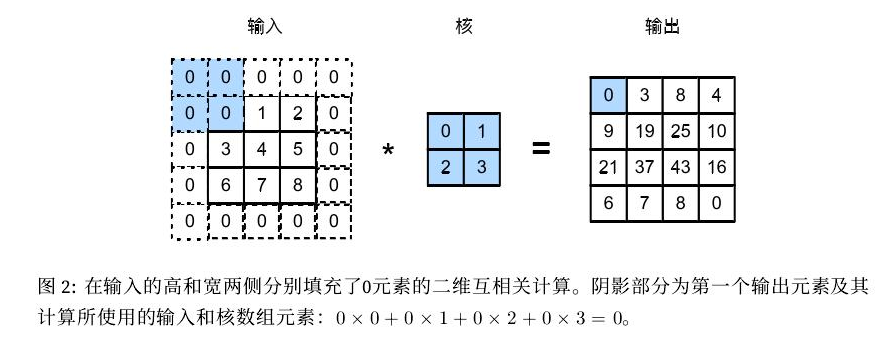
卷积窗口从输⼊数组的最左上⽅开始,按从左往右、从上往下的顺序,依次在输⼊数组上滑动。我们将每次滑动的⾏数和列数称为步幅(stride)
上面的计算过程中,步幅(stride)为1。当然步幅可以设为大于1的数。例如,当步幅为2时,Feature Map计算如下:
多输入通道
到此我们讲了深度为1的卷积层的计算方法,如果深度大于1怎么计算呢?其实也是类似的。 下图展⽰了含2个输⼊通道的⼆维互相关计算的例⼦。在每个通道上,⼆维输⼊数组与⼆维核数组做互相关运算,再按通道相加即得到输出。图中阴影部分为第⼀个输出元及其计算所使⽤的输⼊和核数组元素:
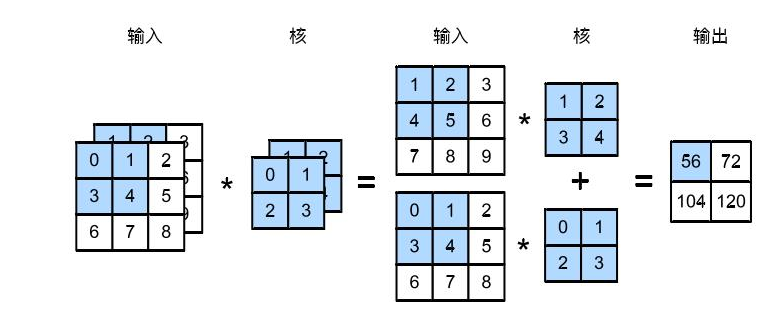
动画演示
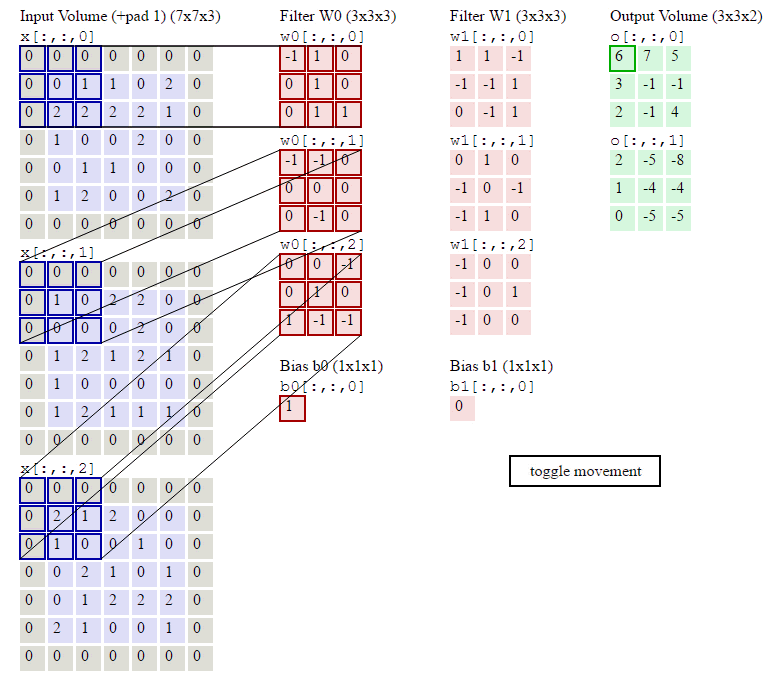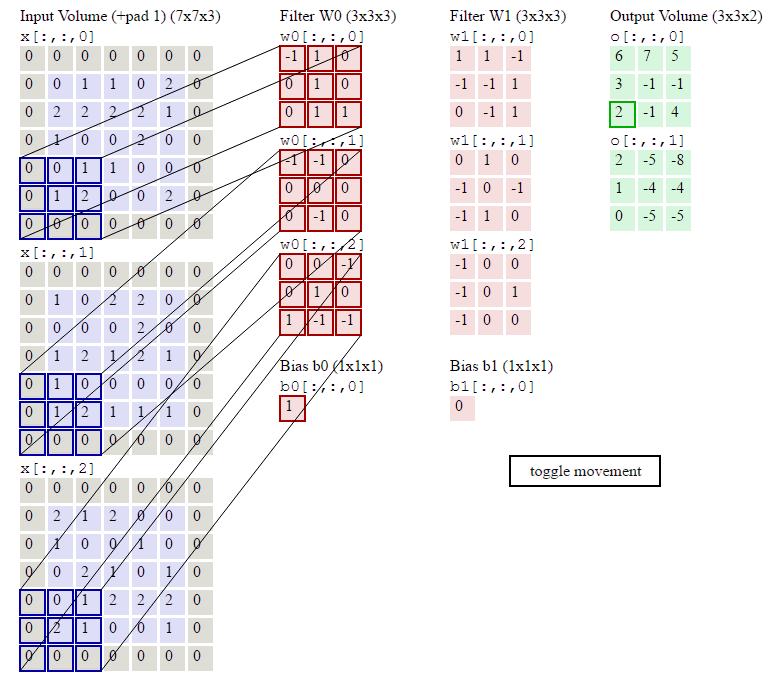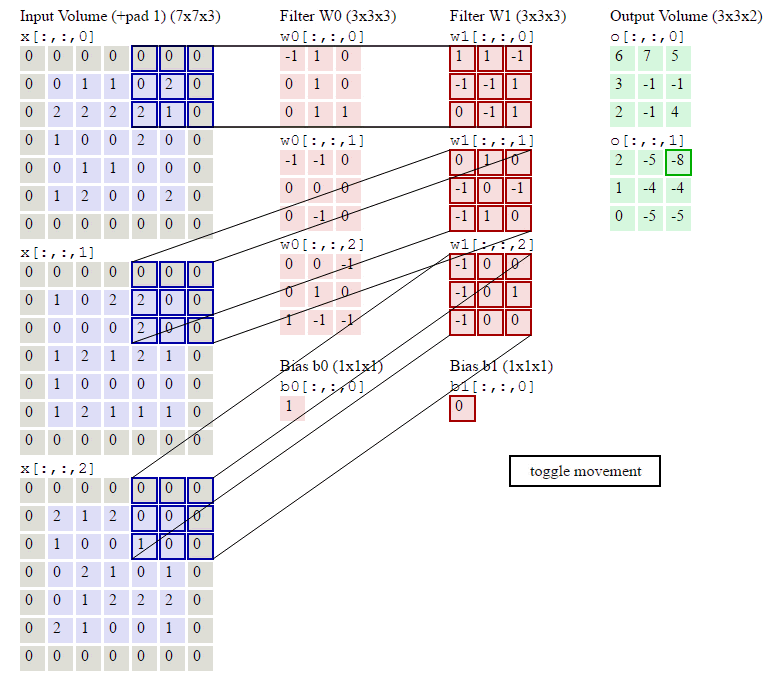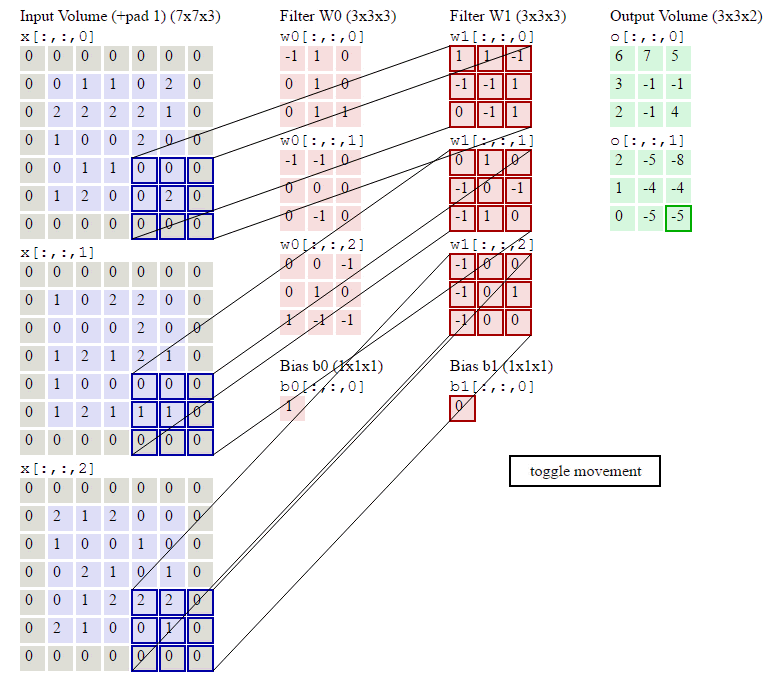
内存需求
CNN 的另一个问题是卷积层需要大量的 RAM,特别是在训练期间,因为反向传播需要在正向传递期间计算的所有中间值。
如果由于内存不足错误导致训练崩溃,则可以尝试减少小批量大小。 或者,您可以尝试使用步幅降低维度,或者删除几个图层。 或者你可以尝试使用 16 位浮点数而不是 32 位浮点数。 或者你可以在多个设备上分发 CNN。
CNN 架构
典型的 CNN 体系结构有一些卷积层(每一个通常跟着一个 ReLU 层),然后是一个池化层,然后是另外几个卷积层(+ ReLU),然后是另一个池化层,等等。 随着网络的进展,图像变得越来越小,但是由于卷积层的缘故,图像通常也会越来越深(即更多的特征映射)。 在堆栈的顶部,添加由几个全连接层(+ ReLU)组成的常规前馈神经网络,并且最终层输出预测(例如,输出估计类别概率的 softmax 层)。
一个常见的错误是使用太大的卷积核。 通常可以通过将两个3×3内核堆叠在一起来获得与9×9内核相同的效果,计算量更少。
多年来,这种基础架构的变体已经被开发出来,导致了该领域的惊人进步。这里就不展开讲了,大家感兴趣可以去找相关的论文和资料深入了解这些流行的CNN架构。
LeNet-5
LeNet-5 架构也许是最广为人知的 CNN 架构。 如前所述,它是由 Yann LeCun 于 1998 年创建的,广泛用于手写数字识别(MNIST)。
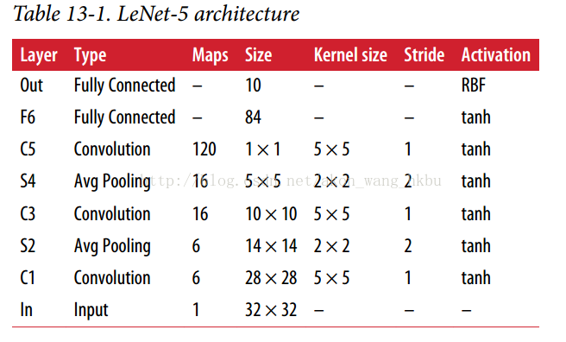
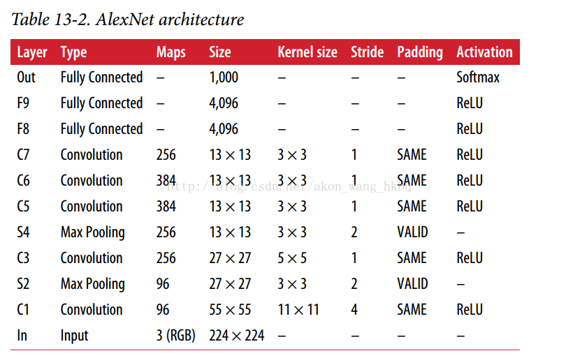
AlexNet
AlexNet CNN 架构赢得了 2012 年的 ImageNet ILSVRC 挑战赛:它达到了 17% 的 top-5 的错误率,而第二名错误率只有 26%! 它由 Alex Krizhevsky(因此而得名),Ilya Sutskever 和 Geoffrey Hinton 开发。 它与 LeNet-5 非常相似,只是更大更深,它是第一个将卷积层直接堆叠在一起,而不是在每个卷积层顶部堆叠一个池化层。
VGG
它名字来源于论⽂作者所在的实验室Visual Geometry Group。VGG提出了可以通过重复使⽤简单的基础块来构建深度模型的思路.
VGG块的组成规律是:连续使⽤数个相同的填充为1、窗口形状为3 × 3的卷积层后接上⼀个步幅为2、窗口形状为2 × 2的最⼤池化层。卷积层保持输⼊的⾼和宽不变,而池化层则对其减半。VGG⽹络同Alex Net和Le Net⼀样,VGG⽹络由卷积层模块后接全连接层模块构成。。全连接模块则跟Alex Net中的⼀样。
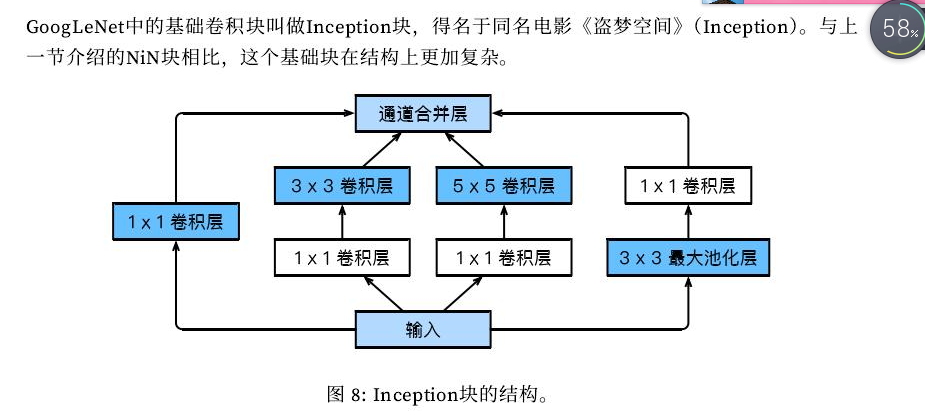
GoogLeNet
GoogLeNet 架构是由 Christian Szegedy 等人开发的。 来自 Google Research,通过低于 7% 的 top-5 错误率,赢得了 ILSVRC 2014 的挑战赛。 这个伟大的表现很大程度上因为它比以前的 CNN 网络更深。 这是通过称为初始模块(inception modules)的子网络实现的,这使得 GoogLeNet 比以前的架构更有效地使用参数:实际上,GoogLeNet 的参数比 AlexNet 少了 10 倍(约 600 万而不是 6000 万)。
ResNet
最后是,2015 年 ILSVRC 挑战赛的赢家 Kaiming He 等人开发的 Residual Network(或 ResNet),该网络的 top-5 误率低到惊人的 3.6%,它使用了一个非常深的 CNN,由 152 层组成。 能够训练如此深的网络的关键是使用跳过连接(skip connection,也称为快捷连接):一个层的输入信号也被添加到位于下一层的输出。 让我们看看为什么这是有用的。
当训练一个神经网络时,目标是使其模拟一个目标函数h(x)。 如果将输入x添加到网络的输出中(即添加跳过连接),那么网络将被迫模拟f(x)= h(x) - x而不是h(x)。 这被称为残留学习
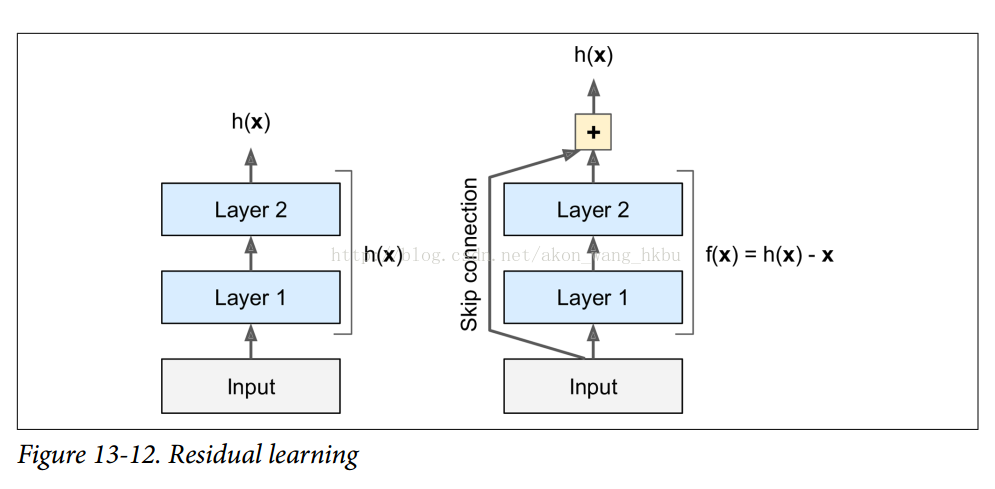
当你初始化一个普通的神经网络时,它的权重接近于零,所以网络只输出接近零的值。 如果添加跳过连接,则生成的网络只输出其输入的副本; 换句话说,它最初对身份函数进行建模。 如果目标函数与身份函数非常接近(常常是这种情况),这将大大加快训练速度。 由于跳过连接,信号可以很容易地通过整个网络。 深度剩余网络可以看作是一堆剩余单位,其中每个剩余单位是一个有跳过连接的小型神经网络。
现在让我们看看 ResNet 的架构(见下图)。 这实际上是令人惊讶的简单。 它的开始和结束与GoogLeNet完全一样(除了没有 dropout 层),而在两者之间只是一堆很简单的残余单位。 每个残差单元由两个卷积层组成,使用3×3的内核和保存空间维度(步幅 1,SAME填充),批量归一化(BN)和 ReLU 激活。
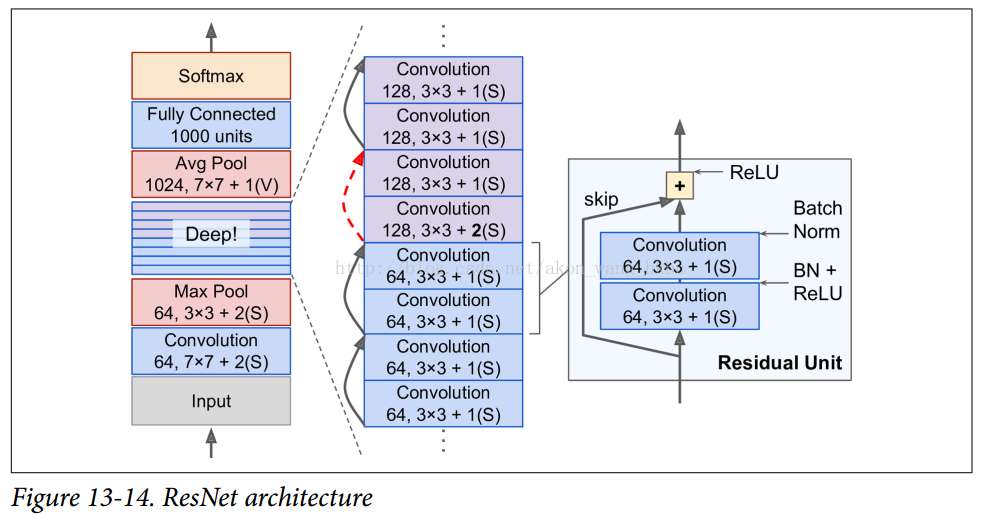
正如你所看到的,这个领域正在迅速发展,每年都会有各种各样的架构出现。 一个明显的趋势是 CNN 越来越深入。 他们也越来越轻量,需要越来越少的参数。 目前,ResNet 架构既是最强大的,也是最简单的,所以它现在应该是你应该使用的 。
Res Net中的跨层连接设计引申出了数个后续⼯作,稠密连接⽹络(Dense Net)是其中一个,Dense Net的主要构建模块是稠密块(dense block)和过渡层(transition layer)。前者定义了输⼊和输出是如何连结的,后者则⽤来控制通道数,使之不过⼤。
还有其他一些架构可供您参考,特别是 VGGNet(2014 年 ILSVRC 挑战赛的亚军)和 Inception-v4(将 GooLeNet 和 ResNet 的思想融合在一起,实现了接近 3% 的 top-5 误差 ImageNet 分类率)。