深度学习（四）：循环神经网络

发表于 | 分类于
字数统计: 4k | 阅读时长 ≈ 15

在本章中，我们将看到循环神经网络背后的基本概念，他们所面临的主要问题（换句话说，在之前中讨论的消失／爆炸的梯度），以及广泛用于反抗这些问题的方法：LSTM 和 GRU cell（单元）。 循环神经网路主要解决带有时序性质的问题。

基本循环神经

看下图中一个简单的循环神经网络图，它由输入层、一个隐藏层和一个输出层组成。我们可以看到，循环神经网络的隐藏层的值s不仅仅取决于当前这次的输入x，还取决于上一次隐藏层的值s（结果向前和向后传播后的上一次这个位置的值）。

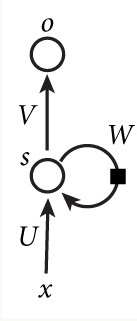
如果我们把上面的图展开，循环神经网络也可以画成下面这个样子：

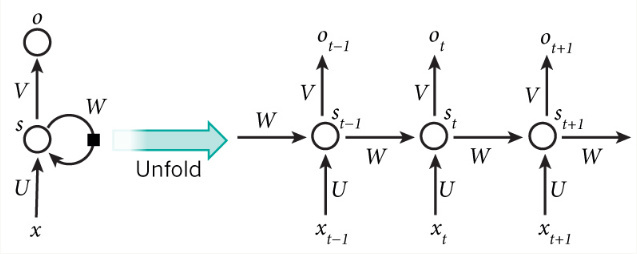
现在看起来就清楚不少了，这个网络在t时刻接收到输入$X_t$之后，隐藏层的值是$S_t$，输出值是$o_t$。关键一点是，$s_t$的值不仅仅取决于$X_t$，还取决于$S_{t−1}$。我们可以使用下面的公式来表示循环神经网络的计算方法： (U,V,W都为权重)

式1是输出层的计算公式，输出层是一个全连接层，也就是它的每个节点都和隐藏层的每个节点相连。V是输出层的权重矩阵，g是激活函数。式2是隐藏层的计算公式，它是循环层。U是输入x的权重矩阵，W是上一次的值st−1st−1作为这一次的输入的权重矩阵，f是激活函数。

从上面的公式可以看出，循环层和全连接层的区别就是多了一个权重矩阵W。

若反复把式2代入带式1，我们将得到：

从上面可以看出，循环神经网络的输出值$o_t$，是受前面历次输入值$x_t$、$x_{t−1}$、$x_{t−2}$…的影响的，这就是为什么循环神经网络可以往前看任意多个输入值的原因。

再来看一个清晰一点的循环神经元层，见下图， 在每个时间步t，每个神经元都接收输入向量$x^{(t)}$和前一个时间步的输出向量$y^{(t−1)}$，如图所示。 请注意，输入和输出都是向量（当只有一个神经元时，输出是一个标量）。

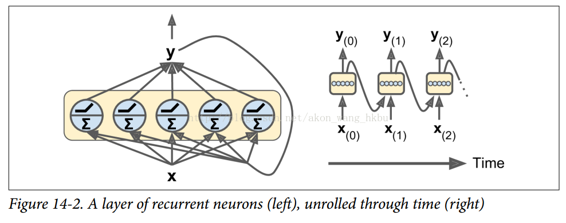
每个循环神经元有两组权重：一组用于输入 $x^{(t)}$，另一组用于前一时间步长 $y^{(t−1)}$的输出。我们称这些权重向量为$w_x$和$w_y$。如下面公式所示（b是偏差项，φ(·)是激活函数，例如 ReLU），可以计算单个循环神经元的输出。

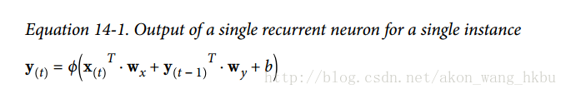
就像前馈神经网络一样，我们可以使用上一个公式的向量化形式，对整个小批量计算整个层的输出。

  • $Y^{(t)}$是$m×n_{neurons}$矩阵，包含在最小批次中每个实例在时间步t处的层输出（m是小批次中的实例数， $n_{neurons}$是神经元数
  • $X^{(t)}$是$m×n_{inputs}$矩阵，包含所有实例的输入的（$n_{inputs}$是输入特征的数量 ）
  • $W_x$是$ n_{inputs}×n_{neurons} $矩阵，包含当前时间步的输入的连接权重的。
  • $W_y$是$n_{neurons}×n_{neurons}$矩阵，包含上一个时间步的输出的连接权重。
  • 权重矩阵$W_x$和$W_y$通常连接成单个矩阵W，形状为$(n_{inputs}+n_{neurons})×n_{neurons}$（见上述公式第二行）
  • b是大小为 $n_{neurons}$的向量，包含每个神经元的偏置项

注意， 在第一个时间步，t = 0，没有以前的输出，所以它们通常被假定为全零。

TensorFlow 中的解释基本 RNN

首先，我们来实现一个非常简单的 RNN 模型，而不使用任何 TensorFlow 的 RNN 操作，以更好地理解发生了什么。 我们将使用 tanh 激活函数创建由 5 个循环神经元的循环层组成的 RNN（如下图所示的 RNN）。

我们将假设 RNN 只运行两个时间步，每个时间步输入大小为 3 的向量。 下面的代码构建了这个 RNN，展开了两个时间步骤：

1
2
3
4
5
6
7
8
9
10
11
n_inputs = 3
n_neurons = 5
X0 = tf.placeholder(tf.float32, [None, n_inputs])
# 充当经过向前向后传播后的下一时刻的输入值
X1 = tf.placeholder(tf.float32, [None, n_inputs]) 
Wx = tf.Variable(tf.random_normal(shape=[n_inputs, n_neurons], dtype=tf.float32))
Wy = tf.Variable(tf.random_normal(shape=[n_neurons, n_neurons], dtype=tf.float32))
b = tf.Variable(tf.zeros([1, n_neurons], dtype=tf.float32))
Y0 = tf.tanh(tf.matmul(X0, Wx) + b)
Y1 = tf.tanh(tf.matmul(Y0, Wy) + tf.matmul(X1, Wx) + b) # 主要理解这句
init = tf.global_variables_initializer()

双向循环神经网络

对于语言模型来说，很多时候光看前面的词是不够的，比如下面这句话：

我的手机坏了，我打算____一部新手机。

可以想象，如果我们只看横线前面的词，手机坏了，那么我是打算修一修？换一部新的？还是大哭一场？这些都是无法确定的，但是如果我们也看到了后面的词是“一部新手机”，那么横线上的词填“买”的概率就大很多了。

而这个在单向循环神经网络是无法建模的，因此我们需要双向循环神经网络，如下图所示：

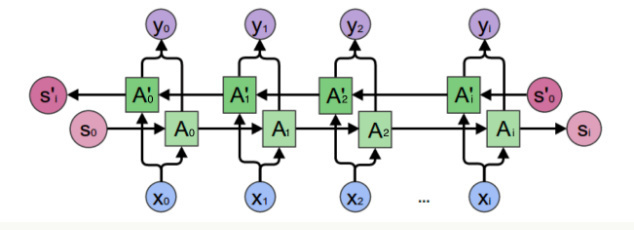
我们先考虑$y_2$的计算，从上图可以看出，双向卷积神经网络的隐藏层要保存两个值，一个A参与正向计算，另一个A′参与反向计算。最终的输出值$y_2$取决于$A_2$和$A_2’$，其计算方法为：

$A_2$和$A_2’$ 则分别计算

现在，我们已经可以看出一般的规律：正向计算时，隐藏层的值$s_t$与$s_{t−1}$有关；反向计算时，隐藏层的值$s_t′$与$s′_{t+1}$有关；最终的输出取决于正向和反向计算的加和。现在，我们仿照式1和式2，写出双向循环神经网络的计算方法：

从上面三个公式我们可以看到，正向计算和反向计算不共享权重，也就是说U和U′、W和W′、V和V′都是不同的权重矩阵。

深度循环神经网络

前面我们介绍的循环神经网络只有一个隐藏层，我们当然也可以堆叠两个以上的隐藏层，这样就得到了深度循环神经网络。如下图所示

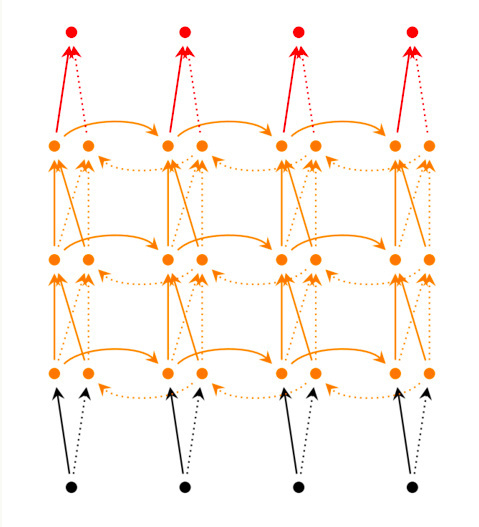
训练 RNN

为了训练一个 RNN，诀窍是在时间上展开（就像我们刚刚做的那样），然后简单地使用常规反向传播（见图 14-5）。 这个策略被称为时间上的标准反向传播（BPTT）。另外可以采用截断式沿时间反向传播算法（BPTT）可以降低循环网络中每项参数更新的复杂度。简而言之，此种算法可以让我们以同样的运算能力更快地定型神经网络 。假设用长度为12个时间步的时间序列定型一个循环网络。我们需要进行12步的正向传递，计算误差（基于预测与实际值对比），再进行12个时间步的反向传递：

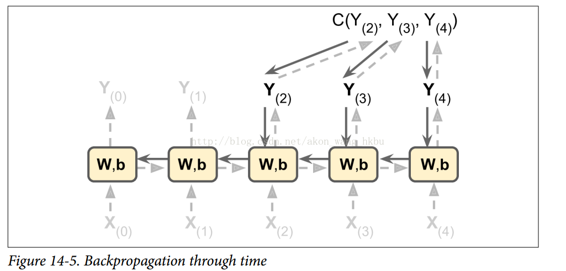
就像在正常的反向传播中一样，展开的网络（用虚线箭头表示）有第一个正向传递。然后使用损失函数评估输出序列$C(Y_{t_{min}},Y_{t_{min+1}},…,Y_{t_{max}})$。其中$t_{min}$ 和$t_{max}$ 是第一个和最后一个输出时间步长，不计算忽略的输出），并且该损失函数的梯度通过展开的网络向后传播（实线箭头）；最后使用在 BPTT 期间计算的梯度来更新模型参数。 请注意，梯度在损失函数所使用的所有输出中反向流动，而不仅仅通过最终输出（截断式传播，例如，在图 14-5 中，损失函数使用网络的最后三个输出Y(2)，Y(3)，和Y(4)，所以梯度流经这三个输出，但不通过Y(0)和Y(1)。而且，由于在每个时间步骤使用相同的参数W和b，所以反向传播将做正确的事情并且总结所有时间步骤。

具体BPTT的解析过程可以看这篇戳我

训练序列分类器

我们训练一个 RNN 来分类 MNIST 图像。 卷积神经网络将更适合于图像分类，但这是一个你已经熟悉的简单例子。 我们将把每个图像视为 28 行 28 像素的序列（因为每个MNIST图像是28×28像素）。 我们将使用 150 个循环神经元的单元，再加上一个全连接层，其中包含连接到上一个时间步的输出的 10 个神经元（每个类一个），然后是一个 softmax 层（见图）。

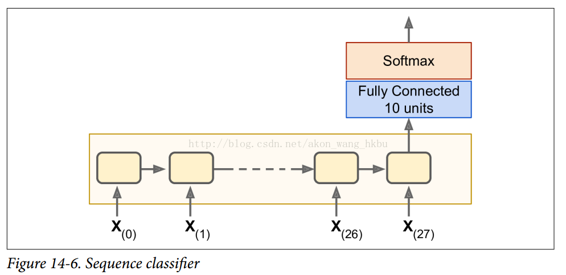
建模阶段非常简单， 它和我们在之前中建立的 MNIST 分类器几乎是一样的，只是展开的 RNN 替换了隐层。 注意，全连接层连接到状态张量，其仅包含 RNN 的最终状态（即，第 28 个输出）。 另请注意，y是目标类的占位符。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
n_steps = 28
n_inputs = 28
n_neurons = 150
n_outputs = 10

learning_rate = 0.001

X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
y = tf.placeholder(tf.int32, [None])

basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons)
outputs, states = tf.nn.dynamic_rnn(basic_cell, X, dtype=tf.float32)

logits = tf.layers.dense(states, n_outputs)
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y,
                                                          logits=logits)
loss = tf.reduce_mean(xentropy)
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
training_op = optimizer.minimize(loss)
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))

init = tf.global_variables_initializer()

现在让我们加载 MNIST 数据，并按照网络的预期方式将测试数据重塑为[batch_size, n_steps, n_inputs]。 我们之后会关注训练数据的重塑。

1
2
3
4
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/")
X_test = mnist.test.images.reshape((-1, n_steps, n_inputs))
y_test = mnist.test.labels

现在我们准备训练 RNN 了。 执行阶段与第 10 章中 MNIST 分类器的执行阶段完全相同，不同之处在于我们在将每个训练的批量提供给网络之前要重新调整。

现在我们准备训练 RNN 了。 执行阶段与第 10 章中 MNIST 分类器的执行阶段完全相同，不同之处在于我们在将每个训练的批量提供给网络之前要重新调整。

1
2
3
4
5
6
7
8
9
10
11
12
13
batch_size = 150

with tf.Session() as sess:
    init.run()
    for epoch in range(n_epochs):
        for iteration in range(mnist.train.num_examples // batch_size):
            X_batch, y_batch = mnist.train.next_batch(batch_size)
            X_batch = X_batch.reshape((-1, n_steps, n_inputs))
            sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
        acc_train = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
        acc_test = accuracy.eval(feed_dict={X: X_test, y: y_test})
        print(epoch, "Train accuracy:", acc_train, "Test accuracy:", acc_test)

输出应该是这样的：

我们获得了超过 98% 的准确性 - 不错！ 另外，通过调整超参数，使用 He 初始化初始化 RNN 权重，更长时间训练或添加一些正则化（例如，droupout），你肯定会获得更好的结果。

你可以通过将其构造代码包装在一个变量作用域内（例如，使用variable_scope("rnn", initializer = variance_scaling_initializer())来使用 He 初始化）来为 RNN 指定初始化器。

为预测时间序列而训练

首先，我们来创建一个 RNN。 它将包含 100 个循环神经元，并且我们将在 20 个时间步骤上展开它，因为每个训练实例将是 20 个输入那么长。 每个输入将仅包含一个特征（在该时间的值）。 目标也是 20 个输入的序列，每个输入包含一个值。 代码与之前几乎相同：

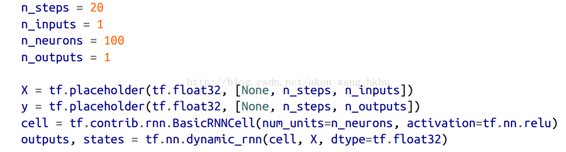
一般来说，你将不只有一个输入功能。 例如，如果你试图预测股票价格，则你可能在每个时间步骤都会有许多其他输入功能，例如竞争股票的价格，分析师的评级或可能帮助系统进行预测的任何其他功能。

在每个时间步，我们现在有一个大小为 100 的输出向量。但是我们实际需要的是每个时间步的单个输出值。 最简单的解决方法是将单元包装在OutputProjectionWrapper中。 单元包装器就像一个普通的单元，代理每个方法调用一个底层单元，但是它也增加了一些功能。Out putProjectionWrapper在每个输出之上添加一个完全连接的线性神经元层（即没有任何激活函数）（但不影响单元状态）。 所有这些完全连接的层共享相同（可训练）的权重和偏差项。 结果 RNN 如图所示

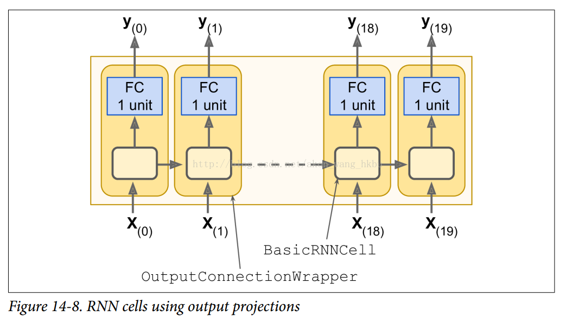
装单元是相当容易的。 让我们通过将BasicRNNCell包装到OutputProjectionWrapper中来调整前面的代码：

1
2
3
cell =tf.contrib.rnn.OutputProjectionWrapper(
    tf.contrib.rnn.BasicRNNCell(num_units=n_neurons,activation=tf.nn.relu),
    output_size=n_outputs)

到现在为止还挺好。 现在我们需要定义损失函数。 我们将使用均方误差（MSE），就像我们在之前的回归任务中所做的那样。 接下来，我们将像往常一样创建一个 Adam 优化器，训练操作和变量初始化操作。（省略）

生成 RNN

到现在为止，我们已经训练了一个能够预测未来时刻样本值的模型，正如前文所述，可以用模型来生成新的序列。

为模型提供 长度为n_steps的种子序列, 比如全零序列，然后通过模型预测下一时刻的值；把该预测值添加到种子序列的末尾，用最后面 长度为n_steps的序列做为新的种子序列，做下一次预测，以此类推生成预测序列。

1
2
3
4
5
sequence = [0.] * n_steps
for iteration in range(300):
    X_batch = np.array(sequence[-n_steps:].reshape(1, n_steps, 1)
    y_pred = sess.run(outputs, feed_dict={X: X_batch}
    sequence.append(y_pred[0, -1, 0]

LSTM 单元

在训练长序列的 RNN 模型时，那么就需要把 RNN 在时间维度上展开成很深的神经网络。正如任何深度神经网络一样，其面临着梯度消失/爆炸的问题，使训练无法终止或收敛。很多之前讨论过的缓解这种问题的技巧都可以应用在深度展开的 RNN 网络：好的参数初始化方式，非饱和的激活函数（如 ReLU），批量规范化（Batch Normalization）， 梯度截断（Gradient Clipping），更快的优化器。

即便如此， RNN 在处理适中的长序列（如 100 输入序列）也在训练时表现的很慢。最简单和常见的方法解决训练时长问题就是在训练阶段仅仅展开限定时间步长的 RNN 网络，一种称为截断时间反向传播的算法。

在长的时间训练过程中，第二个要面临的问题时第一个输入的记忆会在长时间运行的 RNN 网络中逐渐淡去。 那么在一定时间后，第一个输入实际上会在 RNN 的状态中消失于无形。 为了解决其中的问题，各种能够携带长时记忆的神经单元的变体被提出。这些变体是有效的，往往基本形式的神经单元就不怎么被使用了。

首先了解一下最流行的一种长时记忆神经单元：长短时记忆神经单元 LSTM。 可以看下面这篇文章

理解LSTM网络

注：LSTM和GRU单元是近年来RNN成功背后的主要原因之一，特别实在自然语言的应用

-------------Thanks for Reading!-------------