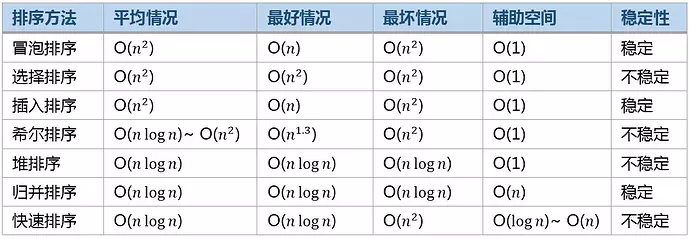
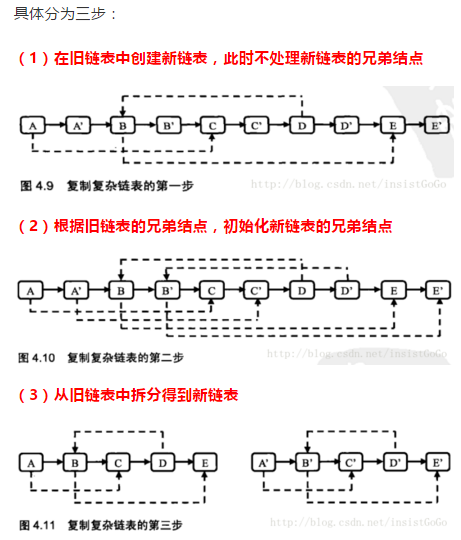
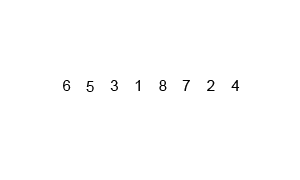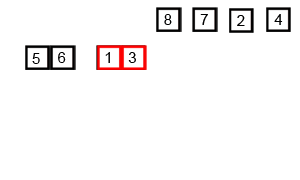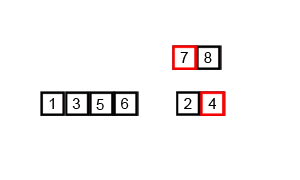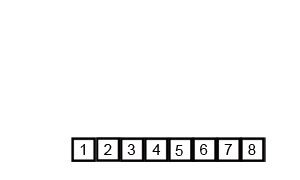基本概念
关联规则
关联规则可以用以下表示:
规则的支持度和置信度是两个规则兴趣度度量,它们分别反映发现规则的有用性和确定性。上诉关联规则
的支持度(表示同时包含A和B的事务占所有事物的比例)为2%,意味所分析的事务的2%显示 计算机和杀毒软件被同时购买。置信度(表示包含A的事务同时也包含B的比例) 60%意味购买计算机的顾客 60%的几率也购买财务管理软件。一般如果关联规则满足最小支持度阈值和最小置信度阈值,则认为关联规则是有趣的,是值得关注的现象。
频繁项集、闭项集、极大项集
设任务相关的数据 D 是数据库事务的集合,每一个事务有一个标识符,称作 TID。设A、B是两个项集,有:
同时满足最小支持度阈值(min_sup)和最小置信度阈值(min_conf)的规则称作强规则
项的集合称为项集。包含 k 个项的项集称为 k-项集。项集的出现频率是包含项集的事务数,简称为项集的频率、支持计数或计数。如果项集满足最小支持度,则称它为频繁项集。频繁 k -项集的集合通常记作 LkLk。一般而言,关联规则的挖掘是一个两步的过程:
1、找出所有频繁项集:根据定义,这些项集出现的频繁性至少和预定义的最小支持计数一样。
2、由频繁项集产生强关联规则:根据定义,这些规则必须满足最小支持度和最小置信度。
从大型数据集中挖掘项集的主要挑战是,这种挖掘常常产生大量满足最小支持度(min_sup)阈值的项集,当min_sup设置的很低的时候尤其如此,这是因为如果一个项集的频繁的(项集每个项计数都满足最小支持度),则它的每个子集都是频繁的。因此,得到的频繁项集的总个数太大了,为了更好的计算和存储,引入了闭频繁项集和极大频繁项集的概念。
- 闭频繁项集:指这个项集X既是频繁项集又是闭项集,闭项集是指不存在真超项集Y和此项集X具有相同的支持度计数
- 极大频繁项集:指这个项集X既是频繁项集又是极大项集,极大项集是指不存在频繁的真超项集Y,它已经是最大规模频繁项集了。
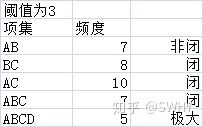
一个举例:(AB项集为非闭是因为和ABC项集具有相同的支持度计数,ABC为非极大是存在频繁项集ABCD)
挖掘频繁项集的方法
Apriori 算法
算法是一种最有影响的挖掘布尔关联规则频繁项集的算法。Apriori 使用一种称作逐层搜索的迭代方法,k项集用于探索(k+1)项集。首先,找出频繁 1-项集的集合。该集合记作 L1。L1用于找频繁 2-项集的集合 L2,而L2用于找L3,如此下去,直到不能找到频繁 k-项集.
所以关键在于须看看如何用频繁项集$L_k$找到频繁项集$L_{k+1}$.具体是由以下两步组成:
1、连接步:为找 $L_k$,通过$L_{k - 1}$与自己连接产生候选 k-项集的集合。假定事务或项集中的项按字典次序排序,如果$L_{k - 1}$它们前(k-2)个项相同的,则可以执行连接操作。
2、剪枝步:连接操作得到$C_k$,$C_k$是 $L_k$的超集,可以通过扫描数据库计算支持度从而在$C_k$里确定$L_k$。然而,$C_k$可能很大,这样所涉及的计算量就很大。为压缩 $C_k$,可以用以下办法使用 Apriori 先验性质:任何非频繁的(k-1)项集都不是可能是频繁 k项集的子集(频繁项集的子集一定是频繁的)。因此,如果一个候选 k项集的(k-1)子集不在 $L_{k - 1}$中 ($L_{k - 1}$包含所有频繁的k-1项集,若某个k-1项集不在里面则是不频繁的),则该候选也不可能是频繁的,从而可以由$C_k$中删除。
一个例子:
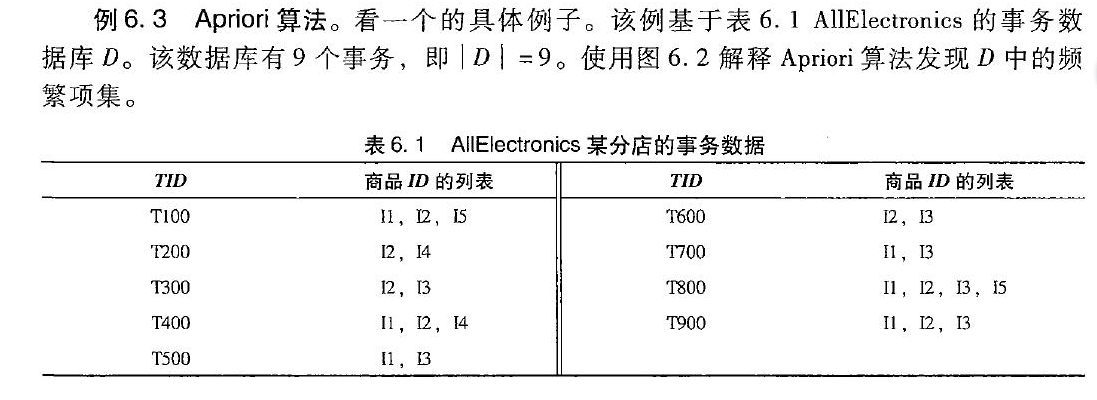
aproori算法过程:假设最小支持度计数为2,即min_sup=2
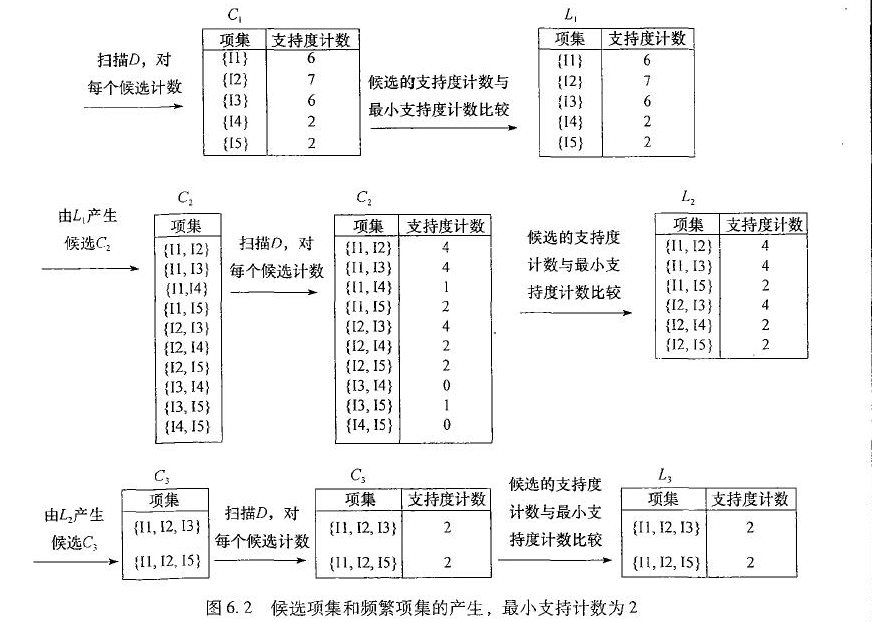
其中,$L_2$连接步寻找$L_3$,要将$L_2$的前(3-2)个相同的项连接起来,得到{I1,I2,I3}, {I1,I2,I5}, {I1,I3,I5}, {I2,I3,I4}, {I2,I3,I5}, {I2,I4,I5},然后执行剪枝步,扫描整个数据库,可以得到剩下的{1,I2,I3}, {I1,I2,I5}。或者使用Apriori 先验性质:举\{I2,I4,I5\}项集为例,\{I2,I4,I5\}的2项子集为\{I2,I4\}, \{I2,I5\} 和 \{I4,I5\}。但\{I4, I5\}不是$L_2$的元素,因此不是频繁的。同理L3L3连接步得到\{I1, I2, I3, I5\}的其中一个3项集\{I2,I3,I5\}不是$L_3$的元素,因此\{I1, I2, I3, I5\}也不是频繁的。
由频繁项集产生关联规则
一旦由数据库 D 中的事务找出频繁项集,由它们产生强关联规则是直接了当的(强关联规则满足最小支持度和最小置信度)。对于置信度,可以用下式,其中条件概率用项集支持度计数表示

FP-growth算法
正如我们已经看到的,在许多情况下,Apriori 的候选产生-检查方法大幅度压缩了候选项集的大小,并导致很好的性能。然而,它可能受两种超高开销的影响:
- 它可能需要产生大量候选项集。例如,如果有 10^4个频繁 1-项集,则 Apriori 算法需要产生多达 10^7个候选 2-项集
- 它可能需要重复地扫描数据库
“ 可以设计一种方法,挖掘全部频繁项集,而不产生候选吗?”一种有趣的方法称作频繁模式增长,或简单地,FP-增长,它采取如下分治策略:将提供频繁项集的数据库压缩到一棵频繁模式树(或 FP-树),但仍保留项集关联信息;然后,将这种压缩后的数据库分成一组条件数据库(一种特殊类型的投影数据库),每个关联一个频繁项,并分别挖掘每个数据库。
FP-growth算法的优点是采用了高级的数据结构。那么这种高级的数据结构是什么呢?实际上就是FP树。 FP树是一种输入数据的压缩表示。他通过把事务映射到FP树上来构造一条路径。这样如果不同事务之间的重叠路径越多,那么就有理由认为他们是频繁项集。由于不同的事务可能会有若干个相同的项,因此它们的路径相互重叠越多,则使用FP树结构获得的压缩效果越好。
FP-growth算法的基本过程1)构建FP数。 2)从FP树中挖掘频繁项集
依然是用之前那个例子:

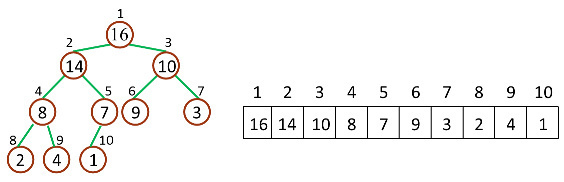
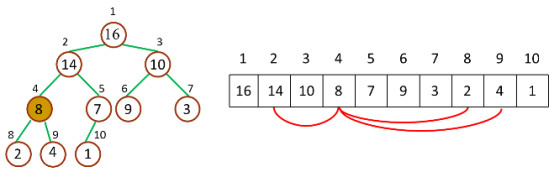
数据库的第一次扫描与 Apriori 相同,它导出频繁项(1-项集)的集合,并得到它们的支持度计数(频繁性)。设最小支持度计数为 2。频繁项的集合按支持度计数的递减序排序。结果集或表记作 L。这样,我们有 L = [I2:7, I1:6, I3:6, I4:2, I5:2]。
然后,FP-树构造如下:首先,创建树的根结点,用“null”标记。二次扫描数据库 D。每个事务中的项按 L 中的次序处理(即,根据递减支持度计数排序)并对每个事务创建一个分枝。例如,第一个事务“T100: I1, I2, I5”按 L 的次序包含三个项\{ I2, I1, I5\},导致构造树的第一个分枝[(I2:1), (I1:1), (I5:1)]。该分枝具有三个结点,其中,I2 作为根的子女链接,I1 链接到 I2,I5 链接到 I1。第二个事务 T200 按 L 的次序包含项 I2 和 I4,它导致一个分枝,其中,I2 链接到根,I4 链接到 I2。然而,该分枝应当与 T100 已存在的路径共享前缀 I2。这样,我们将结点 I2 的计数增加 1,并创建一个新结点(I4:1),它作为(I2:2)的子女链接。一般地,当为一个事务考虑增加分枝时,沿共同前缀上的每个结点的计数增加 1,为随在前缀之后的项创建结点并链接。
按TID顺序T100到T900,不断创建节点和连接,并更新节点的支持度计数,知道完成FP树的构建
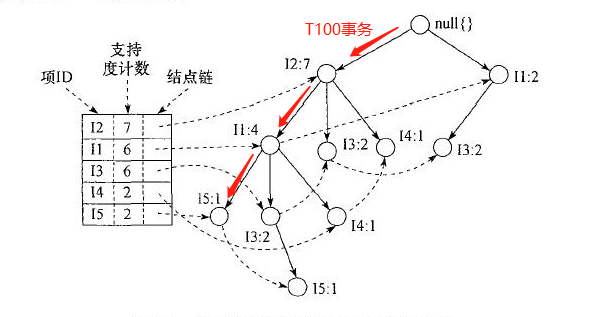
构建好FP树后,开始利用FP树挖掘频繁项集。FP-树挖掘处理如下。由长度为 1 的频繁模式(初始后缀模式)开始,构造它的条件模式基(一个“子数据库”, 由 FP-树中与后缀模式一起出现的前缀路径集组成)。然后,构造它的(条件)FP-树,并递归地在该树上进行挖掘。模式增长通过后缀模式与由条件 FP-树产生的频繁模式连接实现。
FP-树的挖掘总结在表 6.1 中,细节如下。让我们首先考虑 I5,它是 L 中的最后一个项,而不是第一个。其原因随着我们解释 FP-树挖掘过程就会清楚。I5 出现在上图 的 FP-树的两个分枝。(I5 的出现容易通过沿它的结点链到。)它的两个对应前缀路径是[(I2, I1:1)>和<(I2, I1, I3:1)],它们形成I5 的条件模式基。然后以及条件模式基和最小支持度计数构建条件FP树,它的条件 FP-树只包含单个路径[(I2:2, I1:2)] (括号里面为路径形式,给出构建的FP树种每个节点的支持度计数);不包含 I3,因为它的支持度计数为 1,小于最小支持度计数。最后,I5与该路径产生频繁模式的所有组合(I5与路径的所有组合一定是要包含I5的)。组合的支持度计数是根据与结合的节点的支持数决定的。

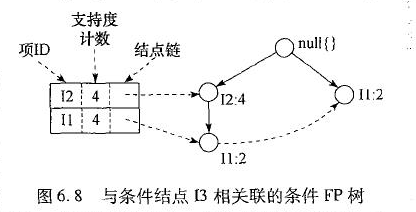
类似的,对于 I4,它的两个前缀形成条件模式基\{(I2 I1:1), (I2:1)\},产生一个单结点的条件 FP-树< I2:2>,并导出一个频繁模式 I2 I4:2。与以上分析类似,I3 的条件模式基是\{(I2 I1:2), (I2:2), (I1:2)\}。它的条件 FP-树有两个分枝< I2:4, I1:2>和< I1:2>,如图 6.9 所示,它产生模式集:\{I2 I3:4, I1 I3:2, I2 I1 I3:2\}.
FP-增长方法将发现长频繁模式的问题转换成递归地发现一些短模式,然后与后缀连接。它使用最不
频繁的项作后缀,提供了好的选择性。该方法大大降低了搜索开销。
使用垂直数据格式挖掘频繁项集
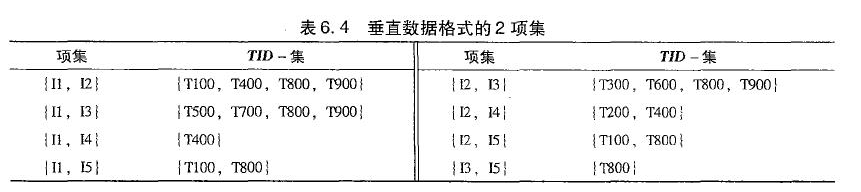
Apriori算法和FP-growth算法都是从TID-项集格式(即\{TID : itemset \})的事务集中挖掘频繁模式,其中TID是事务标识符, 而itemset是事务TID中购买的商品。这种数据格式称为水平数据格式。或者,数据也可以用项-TID集格式(即\{item : TID_set\})表示,这种格式称为垂直数据格式。

通过取每对频繁项的TID集的交,可以在该数据集上进行挖掘。项集的支持度计数为TID-集的元素个数。
强规则不一定是有趣的
大部分关联规则挖掘算法使用支持度-置信度框架。尽管使用最小支持度和置信度阈值排除了一些无兴趣的规则的探
查,仍然会产生一些对用户来说不感兴趣的规则。当A与B是负相关时,规则 A ⇒ B 的置信度有一定的欺骗性。因此,支持度和置信度度量不足以过滤掉无趣的关联规则,为了处理这个问题,可以使用相关性度量来扩充关联规则的支持度-置信度框架。这导致如下形式的相关规则
提升度(lift)
提升度(lift)是一种简单的相关性度量,A和B出现之间的提升度可以通过计算下式得到
如果lift(A,B)值小于1,则A的出现和B的出现是负相关的,意味一个出现可能导致另一个不出现。如果值大于1,则A和B是正相关的,意味着每一个的出现都蕴含另一个的出现。如果结果值等于1,则A和B是独立的,它们之间没有相关性。
使用提升度的相关分析
如果我们要分析如下的关联规则:
且有下面的事务相依表:
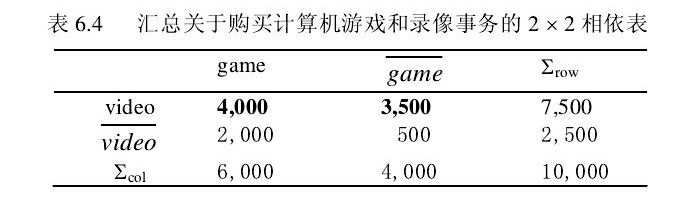

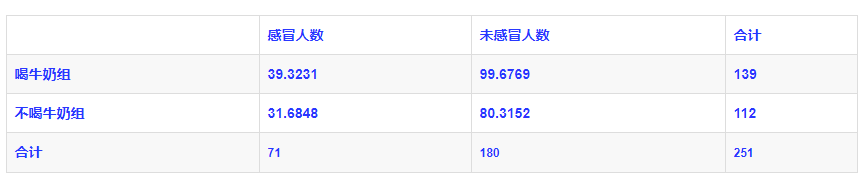
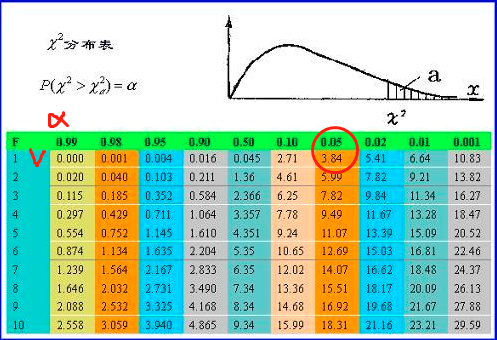
使用卡方检测的相关分析
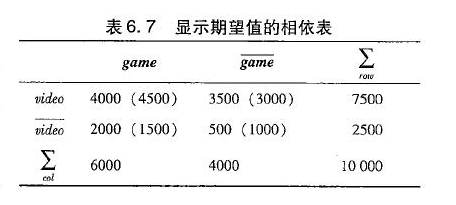

模式评估度量比较
最近,另外一些模式评估度量引起了关注,本书介绍了四种这样的度量:全置信度、最大置信度、Kulczynsji和余弦。然后,比较它们的有效性,并且与提升度和卡方检测$X^2$进行比较。
全置信度:
最大置信度:
Kulczynski:
余弦:
对于评估所发现的模式联系,哪一个度量最好呢?对于零事务提升度和卡方检测效果都不好,零事务是指不包含任何考察项集的事务。典型地,零事务的个数可能远远大于个体的购买的个数,因为许多人都即不买牛奶也不买咖啡。另一方面,上面的新的四种度量都能解决零事务,因为他们的定义都消除了零事务的影响。一般的,推荐Kluc优先。